Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 124

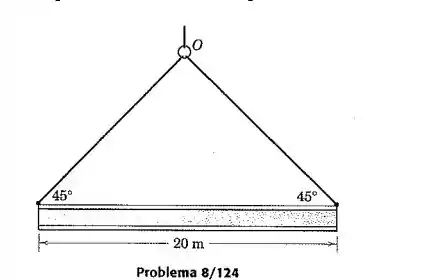
Uma viga I com 20 m está sendo erguida pelo esquema de cabos mostrado. Determine o período τ das pequenas oscilações em torno da conexão O , que se supõe permanecer fixa e em torno da qual os cabos giram livremente. Considere a viga como uma haste esbelta.

Passo 1

Para esse problema vamos usar as relações torque resultante para encontrar a equação do oscilador harmônico para pequenos ângulos θ .

Passo 2

Temos que as únicas forças que colaboram com o torque é a força peso, dada nesse problema por - m ⋅ g ⋅ l 2 . Vemos também que o momento de inércia de nossa superfície é dada na tabela D/3 e tem o valor de I o = 1 12 ⋅ m ⋅ l 2 + m ⋅ l 2 2 . Usando então a equação para torque resultante, temos que

Τ r = - m ⋅ g ⋅ l 2 ⋅ sin ⁡ θ = I o ⋅ θ ¨ = 1 12 ⋅ m ⋅ l 2 + m ⋅ l 2 2 ⋅ θ ¨

- g 2 ⋅ sin ⁡ θ = 1 12 ⋅ l ⋅ θ ¨ + l 4 ⋅ θ ¨ = 1 3 ⋅ l ⋅ θ ¨

θ ¨ + 3 ⋅ g 2 ⋅ l ⋅ sin ⁡ θ = 0

Assumindo θ pequeno, temos que sin ⁡ θ → θ . Assim:

θ ¨ + 3 ⋅ g 2 ⋅ l ⋅ θ = 0

Temos então que ω n = 3 ⋅ g 2 ⋅ l e o período é dado por τ = 2 ⋅ π ω n . Logo

τ = 2 ⋅ π ⋅ 2 ⋅ l 3 ⋅ g = 7.33   s

Resposta

τ = 7.33   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador harmônico amortecido tme um fator Q = 10 . Partindo da posição de equilíbrio, é-lhe comunicada uma velocidade inicial de 5m / s . Verifica-se que a energia total do oscilador diminui numa
Para pequenas partículas em queda livre na atmosfera, a resitência do ar é proporcional à velocidade, ou seja, orientando o eixo z vertocalmente para baixo, é da forma - ρ z ˙ρ0 . Considere a queda li
Um bloco de 1k g , ligado a uma parede vertical por uma mola de massa desprezível e constante elástica 100N / m , inicialmente relaxada, pode deslocar-se sobre uma superfície horizontal com coeficient
88. Dois cilindros homogêneos de raio R e massa total M são conectados ao longo do seu eixo comum por uma barra leve e curta, e estão em repouso sobre uma mesa horizontal. Uma mola cuja constante é k
71. Um oscilador de 200g , dentro de uma câmara de vácuo, oscila com frequência de 2,0H z . Quando a câmara se enche de ar, em 50s a oscilação diminui para 60 % de sua amplitude inicial. Quantas oscil