Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 170

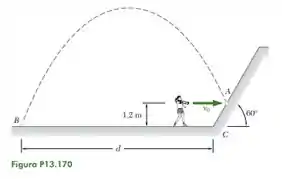
Uma garota arremessa uma bola contra uma parede inclinada a uma altura de 1,2   m . A bola bate na parede em A com uma velocidade horizontal   v 0   de intensidade 15   m / s . Sabendo que o coeficiente de restituição entre a bola e a parede é de 0,9 e desprezando o atrito, determine a distância d da base da parede ao ponto B , no chão, onde a bola quicará depois do rebote na parede.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Pegando a direção paralela a parede, teremos que, pela conservação de momento:

m v   s e n 30 ° = m v '

15 × s e n 30 ° = v '

v ' = 7,5   m / s

Pelo coeficiente de restituição, temos que, na direção perpendicular à parede:

v cos ⁡ 30 ° × e = v '

v ' = 11,69   m / s

Escrevendo a velocidade em função de x   e y ,   teremos:

v x ' = v p e r p ' cos ⁡ 30 ° - v p a r a l e l o ' s e n ( 30 ° )

v x ' = 6,374   m / s

v y ' = v p e r p ' sen ⁡ 30 ° - v p a r a l e l o ' c o s ( 30 ° )

v y ' = 12,34 m s

Passo 2

Agora, aplicaremos as fórmulas de física para calcular a distância pedida. Sabemos que:

y = y 0 + v ' t - g t 2 2

Substituindo:

y = 1,2 + 12,34 t - 9,81 t 2 2

No ponto B ,   temos que:

y B = 0

0 = 1,2 + 12,34 t - 9,81 2 t 2

Resolvendo a equação:

t = 2,61   s

Também sabemos que:

x = x 0 + v ' t

Logo:

x = 16,63   m

Portanto:

d = x B - 1,2 cot ⁡ 60 °

d = 15,94   m

Resposta

d = 15,94   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco de massa m viaja a v 1 na direção θ 1 , mostrada no alto do declive liso. Determine sua velocidade escalar v 2 e sua direção θ 2 quando atingir a base.
A caixa A de 50k g é liberada do repouso sobre a rampa lisa. Depois de deslizar pela rampa atinge a caixa B de 100k g , que está em repouso contra uma mola de rigidez k = 10k N / m . Se o coeficiente
O canhão de mola 5k g repousa sobre a superfície lisa. Ele dispara uma bala de massa 1k g , a uma velocidade v ' = 6m / s relativa ao canhão, na direção mostrada. Se o canhão está originalmente em rep
143. O jato viaja a uma velocidade de 800 km/h, a 30° em relação à horizontal. Se o combustível está sendo gasto a 1,5kg/s, e o motor admite o ar a 200 kg/s, equanto o gás exaurido (ar e combustível )
125. O helicóptero de 10Mg carrega um recipiente contendo 500kg de água, que é usada para combater incêndios. Se ele paira sobre a Terra em uma posição fixa e, em seguida, libera 50kg/s de água a 10m/