Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 79
O guincho sustenta um motor de 125 kgs. Determine a força que a carga produz no membro DB e nomembro FD, que contém o cilindro hidráulico H.
Passo 1
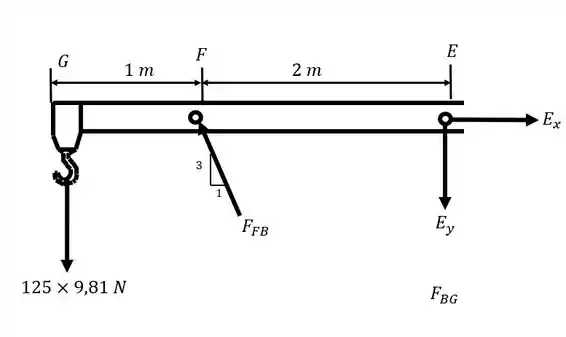
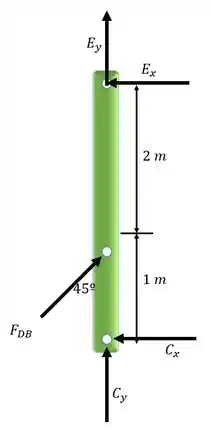
Podemos começar desenhando o diagrama do corpo livre dos membro FB e DB:
Passo 2
Para a resolução dessa questão, o bizu é simplificar e considerar os elementos FB e BD como uma peça única FBD, e substituir as forças por uma só:
Podemos começar aplicando a equação do equilíbrio em relação ao momento no ponto E para membro GFE (primeira figura):
Passo 3
Para o mesmo membro, podemos aplicar as equações do equilíbrio de forças nos eixos x e y:
Passo 4
Podemos começar aplicando a equação do equilíbrio em relação ao momento no ponto C para membro EDC (segunda figura):
Resposta
Exercícios de Livros Relacionados
3.28. Duas esferas, A e B, tem massas iguais e estão eletrostaticamente carregadas, de modo que a força repulsiva que atua entre elas tem uma intensidade de 20m N e está direcionada ao longo da linha
O balde e seu conteúdo têm uma massa de 60k g . Se a corda BAC possui comprimento, determine a distância y até a polia em A para o equilíbrio. Despreze a dimensão da polia.
3.22. Uma força vertical P = 50N é aplicada nas extremidades da corda AB de 0,6m e na mola AC. Se a mola tem um comprimento não deformado de 0,6m , determine o ângulo θ Para o equilíbrio. Considere k
5.57. Os discos lisos D e E possuem um peso de 1k N e 0,5k N , respectivamente. Se uma força horizontal P = 1k N é aplicada no centro do disco E, determine as reações normais nos pontos de contato com
5.54. A barra uniforme AB possui peso de 75N e a mola está descarregada quando θ = 0 ° . Se θ = 30 ° , determine a rigidez k da mola.