Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 51
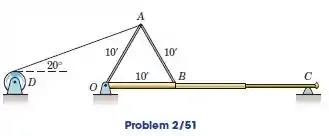
Para levantar o mastro , uma armação leve é presa ao mastro e uma força trativa de é aplicada ao cabo de sustentação pelo guincho em . Calcule o momento desta força trativa em relação à dobradiça no ponto .
Passo 1
Oooi, tudo joinha?
Nesse problema precisamos calcular o momento da força trativa de em relação à dobradiça no ponto . Vamos começar observando a figura:
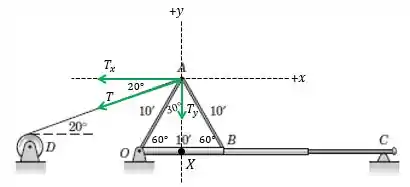
Veja que o triângulo AOB é equilátero, então a medida dos três ângulos internos dele será . O comprimento , ou seja, a altura do triângulo, é distância vertical entre o ponto onde está agindo e o ponto .
A distância horizontal entre o ponto no qual está agindo e o ponto é a metade do segmento , ou seja,
Passo 2
Temos as distâncias, podemos encontrar o momento em relação a . Observe que o momento de é no sentido anti-horário e o de é no sentido horário.
Considerando o sentido anti-horário como positivo:
no sentido anti-horário.