Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 85
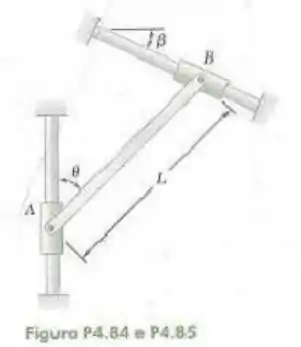
85- Uma haste de massa e comprimento é presa a cursores que podem deslizar livremente ao longo das guias mostradas nas figuras. Sabendo que a haste está em equilíbrio nas figuras. Sabendo que a haste está em equilíbrio e que , determine o ângulo que a haste forma com a vertical as reações em e .
Passo 1
Pela questão anterior encontramos uma equação que correlaciona com e que é:
Como então será:
Passo 2
Agora para resolver a letra nós conseguimos ver que pelo diagrama de corpo livre do cursosr inferior:
E dessa forma conseguimos correlacionar e da seguinte forma:
Como a barra tem massa de então o peso dela será de:
Logo:
Passo 3
Agora pela somatória das forças horizontais nós temos que para atingir o equilíbrio a seguinte equação:
Resposta
Exercícios de Livros Relacionados
A grande tenaz mecânica mostrada na figura é usada para agarrar e erguer uma placa grossa de aço H J de 7500 k g . Sabendo que não ocorre escorregamento entre as garras da tenaz e a placa em H e J , d
Resolva o problema 6.157 considerando que a força P de 9 k N atua horizontalmente para a direita θ = 0 ° .
No sistema de engrenagens planetária mostrado na figura, o raio da engrenagem central A é a = 18 m m , o raio das engrenagens planetárias é b e o raio da engrenagem externa E é a + 2 b . Um binário no
As engrenagens D e G estão rigidamente presas a eixos que são apoiados por mancais sem atrito. Se r d = 90 m m e r c = 30 m m determine a o binário M 0 que deve ser aplicado para manter o equilíbrio,
67. Determine as reações em B e D quando b = 120m m :