Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 84
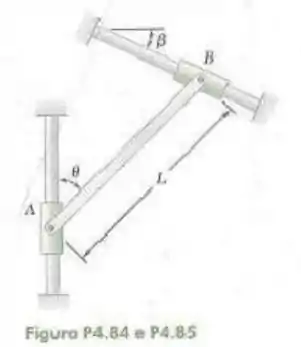
84- Uma haste delgada de comprimento é presa a cursores que podem deslizar livremente ao longo das guias mostradas na figura. Sabendo que a haste está em equilíbrio, deduza uma expressão para o ângulo em termos do ângulo .
Passo 1
Como a força faz uma força normal ao cursor superior nós podemos escrever o diagrama de corpo livre do corpo inferior da seguinte forma:
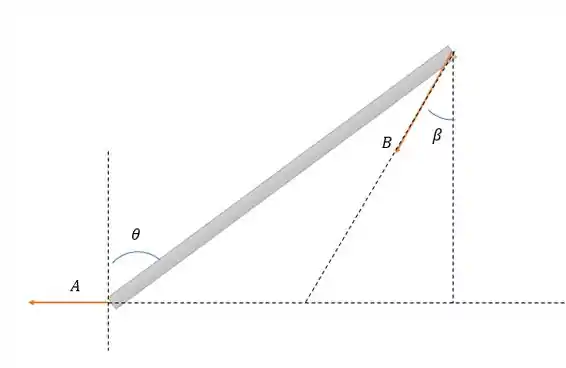
Para que o corpo esteja em equilíbrio, pela teoria das três forças, temos que a força peso encontra e na horizontal da seguinte forma:
Passo 2
Pela figura conseguimos correlacionar e pela seguinte expressão:
Logo:
Resposta
Exercícios de Livros Relacionados
68. Determine as reações em B e C quando a = 38m m :
69. Um caixote de 50k g é preso a uma viga de rolamento mostrado na figura. Sabendo que a = 1,5m , determine ( a ) tração no cabo C D , ( b ) a reação em B .
70. Resolva o problema 4.69 , considerando a = 3,0m .
72. Determine as reações em A e D quando β = 30 ° .
71. A extremidade de uma haste A B apoia no canto A e a outra extremidade é presa na corda B D . Se a haste suporta uma carga de 160N no ponto médio C , encontre a reação em A e a tração na corda: