Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 56
A haste uniforme tem comprimento e peso . Ela é apoiada em uma extremidade por uma parede lisa e na outra extremidade por uma corda com comprimento , presa à parede conforme mostra a figura. Determine a extensão para que haja equilíbrio.
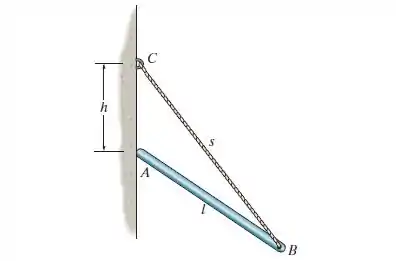
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Nosso objetivo aqui é determinar a altura máxima para que haja equilíbrio. Então, se estamos falando de equilíbrio, as equações abaixo são válidas.
Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Então, o nosso diagrama de equilíbrio será:
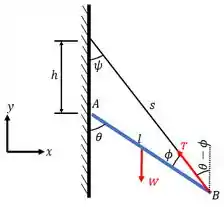
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Para resolvermos esta questão, precisamos obter relações entre as forças (peso e tração) e entre os ângulos da geometria.
Vamos começar avaliando o equilíbrio pela soma dos momentos em torno do ponto , pois assim eliminamos esta incógnita da nossa análise. Portanto,
A segunda relação de equilíbrio que iremos utilizar é: . Portanto,
Só que nós sabemos que . Logo,
E paramos por aqui.
Passo 3
Até agora nós obtivemos relações entre ângulos e entre forças, mas nada ainda que relacione os comprimentos , e .
A nossa primeira relação para isto surge da lei dos senos. Ela nos diz que:
Só que, no final do Passo 2 não obtivemos que , então,
Passo 4
Para finalizarmos a questão, vamos aplicar a lei dos cossenos ao nosso triângulo. Mas, antes disto, é importante percebermos que:
Portanto,
E então,
E assim finalizamos a nossa questão!