Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 30
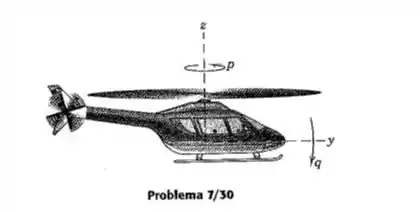
O helicóptero está baixando o nariz na taxa constante q rad/s. Se as hélices do rotor giram na velocidade constante p rad/s, escreva a expressão para a aceleração angular do rotor. Suponha que o eixo y está preso à fuselagem e apontando para a frente, perpendicular ao eixo do rotor.
Passo 1
Primeiramente com o auxílio da regra da mão direita vamos calcular as componentes da velocidade angular(teremos então.
Passo 2
Derivando ômega obtemos que pela equação 7/5 obtemos.
Resposta
Exercícios de Livros Relacionados
O tronco de cone é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia I x e expresse o resultado em termos da massa total m do tronco. O tronco tem uma densidade c
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o momento de inércia em relação ao eixo x e expresse o resultado em termos da massa total m do paraboloide. O materia
O paraboloide é formado girando-se a área sombreada em torno do eixo x . Determine o raio de giração k x . A densidade do material é ρ = 5 Mg/m3.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do semielipsoide.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do sólido.