Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 56

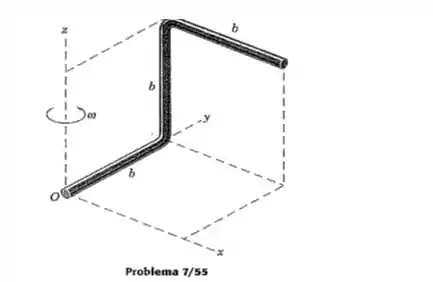
Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g   dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.

Passo 1

Para esse problema nós usaremos o resultado da equação 7/14 que diz:

H p = H G + r - × G onde H p   é o momento de inércia que nós calculamos no item 7/55

Logo H G = H p - r - × G .

Onde G = m ω × r - momento linear deste objeto no centro de massa.

Passo 2

As componentes do centro de massa ficam:

r - = ∑ m r M

3 ρ b = M é a massa total do sistema de barras

r - x = ρ * b 0 + 0 + b 2 3 ρ b = b 6

r - y = ρ * b b 2 + b + b 3 ρ b = 5 6 b

r - z = ρ * b 0 + b 2 + b 3 ρ b = 1 2 b

r - = ( b 6 i + 5 6 * b j + 1 2 * b k )   m

Passo 3

Agora calculando G nós ficamos com:

v = ω × r -

v = ω k × b 6 i + 5 6 * b j + 1 2 * b k = ω * b 6 ( - 5 i + j )

r - × m ω × r - = m * b 6 i + 5 6 * b j + 1 2 * b k × ( ω * b 6 - 5 i + j = )

= ρ b 3 ω 4 * ( - i - 5 j + 2 * b 3 k )

Podemos pôr fim calcular o momento angular no centro de massa:

H G = H p - r - × G

H p = ρ b 3 ω - 1 2 i ^ + 3 2 j ^ + 8 3 k ^ calculado anteriormente no item 7/55

H G = ρ b 3 ω - 1 2 i ^ + 3 2 j ^ + 8 3 k ^ - ρ b 3 ω 4 * - i - 5 j + 2 * b 3 k =

= ρ b 3 ω - 1 2 i ^ - 3 2 j ^ + 8 3 k ^ + 1 4 i ^ + 5 4 j ^ - 13 6 k ^

H G = ρ b 3 ω ( - 1 4 i ^ - 1 4 j ^ + 1 2 k ^ )

Resposta

H G = ρ b 3 ω ( - 1 4 i ^ - 1 4 j ^ + 1 2 k ^ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina de 4 kg é suportada horizontalmente por uma mola em A e uma corda em B. Determine a aceleração angular da barra e a aceleração do centro de massa da barra no instante que a corda em B é c
A bobina uniforme está apoiada em dois roletes em A e B. Determine a força constante P que tem de ser aplicada ao cabo a fim de desenrolar 8 m de cabo em 4 s partindo do repouso. Também calcule as for
A pá única PB do ventilador tem uma massa de 2 kg e um momento de inércia I G = 0,18 kg.m² em relação a um eixo passando pelo seu centro de massa G. Se a pá é submetida a uma aceleração angular α = 5
A roda de 150 kg tem um raio de giração em relação a seu centro de massa O de k O = 250 mm. Se ela gira no sentido anti-horário com uma velocidade angular ω = 1200 rev/min e a força de tração aplicada
Determine a posição r P do centro de percussão P da barra fina de 5kg. (Ver problema 17.66.) Qual é a componente horizontal da força que o pino em A exerce sobre a barra quando ela é atingida em P com