Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 54
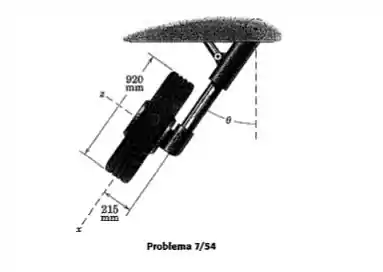
O trem de pouso de uma aeronave, visto de frente, está sendo recolhido imediatamente após a decolagem, e a roda está girando na taxa correspondente à velocidade de decolagem de 200 . A roda de tem um raio de giração em relação a seu eixo z de 370 mm. Despreze a espessura da roda e calcule a quantidade de movimento angular da roda em relação a G e em relação a A para a posição em que está aumentando na taxa de 30º por segundo.
Passo 1
Primeiramente temos que separar o trem de pouso em duas partes, a primeira parte e a haste que segura as rodas que podemos aproximar para uma um cano fino, e a segunda parte são as rodas que tem formato circular.
Para essa configuração x-y-z são os eixos de inercia principais, pois está centrado no centro do círculo, logo para esse sistema de coordenadas nós podemos abusar da simetria circular que implica em:
e teremos também devido a essa simetria
Passo 2
O momento de inercia de um círculo no seu eixo principal é tabelado onde sua coordenada para provar isso podemos utilizar 7/10 onde onde onde e a densidade linear de massa e dl um elemento de largura.
Assim:
Temos também
Entretanto podemos seguir o caminho braçal utilizando a equação 7/10, mas é notória que a simetria do problema facilita sua resolução.
Por fim devemos calcular as componentes da velocidade angular (
Do enunciado nós temos que varia a uma taxa constante de 30º por segundo que em radianos fica se utilizarmos a regra da mão direita veremos que sua direção é j.
Não temos rotação em x logo
Por fim em z nós teremos o giro devido a velocidade(v) do avião
( converta a velocidade para metros/s )
Portanto:
Passo 3
Para o eixo A nós usaremos o teorema dos eixos paralelos para calcular as componentes do tensor de inercia:
Note que a única coisa que muda de um referencial para o outro é a coordenada y logo a única mudança ser em .
Resposta