Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 2
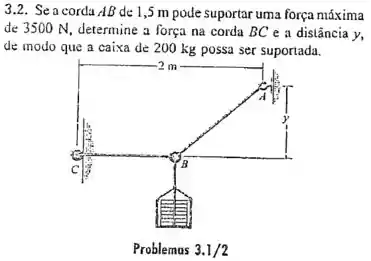
Passo 1
Vamos fazer o diagrama de corpo livre para a agola :
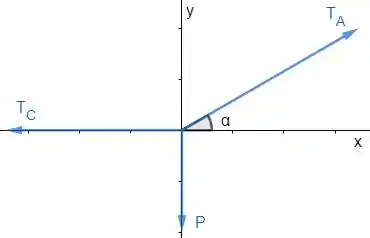
Passo 2
Como tudo isso ai tem que estar parado, a soma de forças em e em deve ser zero.
Vamos decompor as forças em :
O valor de pode ser encontrado através de relações trigonométricas:
A equação fica:
Sabemos os valores de e , além disso o enunciado nos diz que a corda AB suporta uma tração de , então vamos usa-la na equação para descobrir o mínimo:
Passo 3
Agora vamos decompor as forças em e montar a e equação para esse eixo:
No passo dois descobrimos , então podemos descobrir o valor de , do passo anterior sabemos que:
Então
Substituindo e na equação vamos ter:
Resposta
Exercícios de Livros Relacionados
70. Resolva o problema 4.69 , considerando a = 3,0 m .
72. Determine as reações em A e D quando β = 30 ° .
71. A extremidade de uma haste A B apoia no canto A e a outra extremidade é presa na corda B D . Se a haste suporta uma carga de 160N no ponto médio C , encontre a reação em A e a tração na corda:
74. Um rolete de 160N e 200m m de diâmetro, para ser usado em um piso de cerâmica, está apoiado diretamente sobre a base abaixo do piso, tal como mostra a figura. Sabendo que a espessura de cada ladri
72. Determine as reações em A e B quando beta = 30 ° .