Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 70
70. Resolva o problema , considerando .
Passo 1
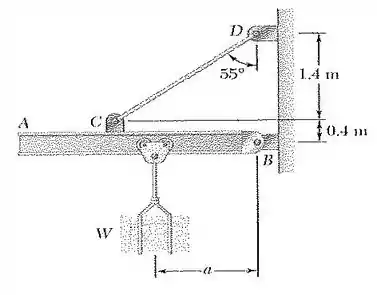
Bom! Primeiramente façamos o esboço do problema, considerando o sistema de três forças que nele estará presente. As forças , e se interceptarão em um ponto em comum, que chamaremos de :
E em seguida, calculemos a tangente de a partir do segmento :
Passo 2
Agora que já sabemos o valor do ângulo , vamos fazer o triângulo de forças para o nosso sistema com as forças , e :
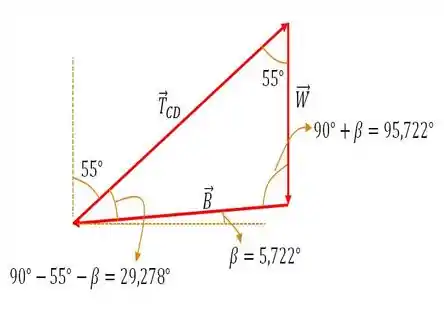
Onde o peso é dado por:
E para achar o valor das forças e , basta usar a lei dos senos:
Primeiro para a força :
E depois para a força :
Resposta
Exercícios de Livros Relacionados
Os membros de um suporte são conectados por um pino na junta O. Determine as intensidades de F 1 e F 2 para o equiíbrio. Considere θ = 60 ° .
A ferramente mostrada é usada para endireitar peças torcidas ao final de uma montagem com madeira. Se a força P = 150N é aplicada ao cabo como mostrado, determine as forças normais aplicadas à garra n
Calcule o módulo da força suportada pelo pino em B no dispositivo em curva, carregado e apoiado como mostrado.
A acrobata de 50k g pedala seu monociclo sobre o cabo esticado, mas ligeiramente elástico. Se a deflexão no centro do vão de 18m vale 75m m , determine a força trativa no cabo. Despreze os efeitos dos
A barra uniforme de 5m e massa de 100k g é articulada em O e impedida de girar mais do que 30 ° no plano vertical pelo rolete fixo em A . Calcule o módulo da força total suportada pelo pino em O .