Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 69
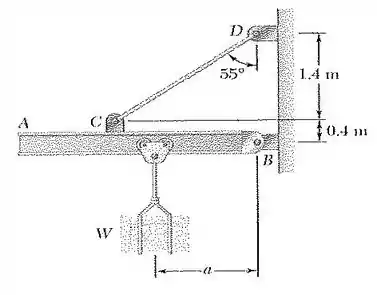
69. Um caixote de é preso a uma viga de rolamento mostrado na figura. Sabendo que , determine tração no cabo , a reação em .
Passo 1
Fala galerinha, bora matar essa questão de estática?
Bom a gente precisa encontrar o que faz essa viga ficar em pé, que são as reações no cabo CD e no pino B. Já te digo de cara pra você não sair fazendo as equações de equilíbrio sem antes separar essa viga e desenhar seu diagrama de corpo livre e é o que faremos.
Note que o pino C tá localizado acima da viga e tem uma distância de 0,4m até o meio da viga onde age a reação HB.
Daqui em diante a gente vai usar as equações de equilíbrio das forças e dos momentos pra encontrar as reações, um bizu é buscar a equação que tem menos incógnitas.
Passo 2
Bom, analisando nossas equações a mais promissora é a do somatório dos momentos. O motivo é que a gente tem a chance de eliminar algumas incógnitas com ela.
O ponto que elimina 2 incógnitas é o ponto B, sendo assim, considerando o sentido anti-horário positivo temos.
Eita mas quem é essa galera toda que apareceu?
O a é do enunciado e vale 1,5m.
Bom, W é o peso do caixote dado por:
X é a medida do pino B ao ponto C e pode ser encontrada pensado na relação trigonométrica do nosso triângulo.
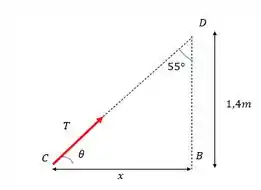
Y é a medida do centro da viga até o pino C e é:
As componentes Ty e Tx são as decomposições da força T do cabo. Aqui a gente pode decompor tanto através do 55 graus quanto através do , aqui nós vamos fazer pelo .
E pelo triângulo da figura a gente vê que:
Assim, susbstituindo:
E voltando enfim pra nossa equação do inicío do passo, a gente pode substituir todo mundo.
E enfim.
Passo 3
Agora pro item b, a questão pede pra gente encontrar a reação no pino B. Como temos o valor da tração no cabo, vai ser tranquilo. Vamos usar as equações de equilíbrio das forças e resolver essa parada!
Substituindo:
E a reação vertical a gente acha fazedo:
Substituindo:
Como o exercício pede a reação em B, vamos tirar a resultante entre as reações vertical e horizontal no pino B.