Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 139

Um homem está parado na plataforma em O e corre para fora na dreção da beira da plataforma de tal maneira que, quando eles está em A, y = 1,5 m, seu centro de massa tem uma velocidade de 0,6 m/s e uma aceleração de 0,9 m/s2 , ambas medidas em relação à plataforma e direcionadas ao longo do eixo y positivo. Se a plataforma tem os movimentos angulares mostrados, determine a velocidade e a aceleração de seu centro de massa nesse instante.

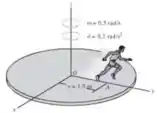
Passo 1

Para a resolução desse exercício, iremos utilizar a análise do movimento relativo usando um sistema de eixos em rotação. O eixo de rotação de referência x y z está coincidindo com o eixo X Y Z , como mostra a figura abaixo:

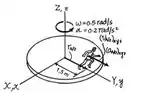
Analisando a figura, temos:

v O = a o = 0 Ω = 0,5 k   r a d / s Ω ˙ = α = 0 , 2 k   r a d / s 2

Do enunciado, temos:

v A / O x y z = 0,6 j   m / s a A / O x y z = 0,9 j   m / s 2 r A / O = 1,5 j   m

Passo 2

Para encontrarmos a velocidade do ponto A, iremos utilizar a fórmula da velocidade relativa abaixo:

v A = v O + Ω × r A / O + v A / O x y z

Então,

v A = 0 + 0,5 k × 1,5 j + 0,6 j = ( - 0,75 i + 0,6 j )   m / s

Passo 3

Agora que conseguimos encontrar o valor da velocidade, basta encontrarmos o valor da aceleração. Para isso, utilizaremos a fórmula abaixo:

a A = a O + Ω ˙ × r A / O + Ω × Ω × r A / O + 2 Ω × v A / O x y z + a A / O x y z = 0 + 0,2 k × 1,5 j + 0,5 k × 0,5 k × 1,5 j + 2 . 0,5 k × 0,6 j + 0,9 j = - 0,3 i + - 0,375 j + - 0,6 i + 0,9 j = - 0,9 i - 1,275 j   m / s 2

Resposta

v A = ( - 0,75 i + 0,6 j )   m / s

a A = - 0,9 i - 1,275 j   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na posição mostrada a barra DC está girando no sentido anti-horário na taxa constante N = 2 r a d / s . Determine a velocidade angular ω e a aceleração angular α de EBO nesse instante.
O mecanismo da roda de Genebra é utilizado em um sistema de empacotamento para converter o movimento angular constante em movimento angular intermitente. A roda em estrela A realiza um sexto de uma re
Um brinquedo em um parque de diversões consiste de um braço em rotação A B tendo uma velocidade angular constante ω A B = 2r a d / s em torno do ponto A e um carrinho montado na extremidade do braço q
O mecanismo de “retorno rápido” consiste de uma manivela A B , o bloco deslizante B e o membro com ranhura C D . Se a manivela tem o movimento angular mostrado, determine o movimento angular do membro
O mecanismo de retorno rápido consiste da manivela C D e do braço com ranhura A B . Se a manivela gira com a velocidade angular e a aceleração angular no instante mostrado, determine a velocidade angu