Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 197

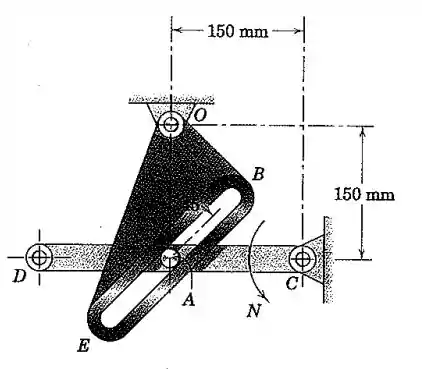
Na posição mostrada a barra DC está girando no sentido anti-horário na taxa constante N = 2 r a d / s . Determine a velocidade angular ω e a aceleração angular α de EBO nesse instante.

Passo 1

Bom pessoal, quando temos uma questão com deslizamento em ranhuras, pegamos um ponto P pertencente ao elemento ranhurado que coincide com o ponto A da barra CD. Assim, temos dois pontos com diferentes velocidades e a velocidade relativa entre estes pontos deve estar na direção da ranhura.

Vamos fazer um esboço do mecanismo representando seus vetores velocidade:

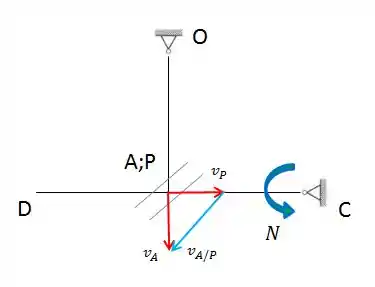
Beleza! Vamos agora calcular a velocidade de A:

v A = N × r A C = 2 × 0,15 = 0,3   m / s

Considerando que a ranhura está a 45 graus da horizontal, então temos que:

v A = v P = 0,3   m / s

v A / P = v r e l = 2 v A = 0,424   m / s

E ainda podemos calcular a velocidade angular do elemento EBO:

ω = v P r P O = 0,3 0,15 = 2 r a d s ,   s e n t i d o   a n t i   h o r á r i o

Passo 2

Agora, vamos para o cálculo das acelerações.

A aceleração do ponto A pode ser representada por:

a A = a A n + a A t

Onde:

a A n = - r A C N 2 = - - 0,15 i ^ 2 2 = 0,6 i ^   m / s 2

a A t = 0 ,     p o i s   N   é   c o n s t a n t e

De forma semelhante, podemos calcular a aceleração do ponto P a partir de PO:

a P = a P n + a P t

Onde:

a P n = - r P O ω 2 = - - 0,15 j ^ 2 2 = 0,6 j ^   m / s 2

a P t = α × r P O , = 0,15 α   i ^   r a d / s

Agora, vamos aplicar a equação geral da aceleração relativa entre os pontos A e P:

a A = a P + α × r A P + ω × ω × r A P + 2 ω × v r e l + a r e l

Como P e A possuem a mesma coordenada, r A P = 0

a A = a P + 2 ω × v r e l + a r e l

Onde:

2 ω × v r e l = 2 2 k ^ × 0,424 - c o s 45   i - s e n 45   j = 1,2 ( i - j )   m / s 2

Outro detalhe importante: Assim como v r e l , a a r e l também deve estar na direção de seu movimento, isto é, da ranhura.

Então a expressão fica assim:

0,6 i ^ = 0,6 j ^ + 0,15 α   i ^ + 1,2 i - j + a r e l ( c o s 45   i ^ + s e n 45   j ^ )

Decompondo nas direções:

0,6 i ^ = 0,15 α   i ^ + 1,2 i + a r e l ( c o s 45   i ^ )

0 = 0,6 j ^ + 1,2 - j + a r e l ( + c o s 45   j ^ )

Resolvendo o sistema, achamos:

a r e l = 0,85   m / s

α = - 8 k ^   r a d / s 2

Resposta

ω = 2 k ^ r a d s

α = - 8 k ^ r a d s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o bloco deslizante B está se deslocando para a direita com a velocidade e aceleração mostradas. Determine a aceleração angular da roda nesse instante.
No dado instante, o membro AB tem o movimento angular mostrado. Determine a velocidade e a aceleração do bloco deslizante C nesse instante.
O cilindro hidráulico se estende com uma velocidade v A = 1,5m / s e uma aceleração a A = 0,5m / s 2 . Determine a aceleração angular do membro ABC e a aceleração da extremidade C no instante mostrado
O cilindro hidráulico D se estende com a velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de A no instante mostrado.
O cilindro hidráulico D se estende com uma velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de C no instante mostrado.