Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 160
O mecanismo da roda de Genebra é utilizado em um sistema de empacotamento para converter o movimento angular constante em movimento angular intermitente. A roda em estrela realiza um sexto de uma revolução para cada revolução compreta da roda motriz e da guia . Para fazer isto, o pino , que está fixo a , desliza para dentro de uma das ranhuras radiais de , dessa maneira girando a roda , e em seguida deixa a ranhura. Se tem uma velocidade angular constante , determine e da roda no instante mostrado.
Passo 1
Como o mecanismo em questão possui uma ligação através do ponto , é possível encontrar as informações de velocidade e aceleração neste ponto do pino transmissor e, então, fazer a análise de apenas uma das ranhuras da roda em estrela para verificar a transmissão da velocidade e da aceleração do pino para a roda.
Então, a velocidade de em relação a poderá ser determinada a partir de:
E a aceleração é:
Onde:
distância de até
velocidade angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem;
aceleração angular do sistema de eixos localizado no ponto de interesse em relação ao sistema de referência de origem.
Passo 2
Fazendo o diagrama de corpo livre (DCL) de uma das partes da roda em estrela tem-se:
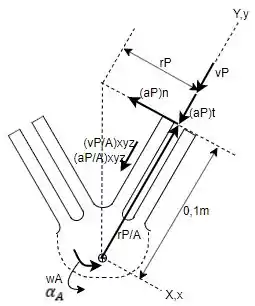
Para determinar a velocidade do pino , é possível determina-la através da simples relação com a aceleração angular sob a qual ele é submetido, ou seja:
Isso se deve ao fato de o pino estar girando em torno de um ponto fixo, então o ponto possui velocidade nula.
representa o raio do trajeto circular pelo qual o pino se move que é dado por:
Então a velocidade será de:
Enquanto que a sua aceleração será dada por:
Passo 3
Sendo assim, tendo essas variáveis determinadas juntamente com os valores previamente fornecidos pelo exercício, se torna possível fazer o cálculo dos valores desejados da roda em estrela .
Portanto, aplicando a outra equação da velocidade em , tem-se:
Tal que a velocidade angular da referência medida a partir do referencial será a soma das velocidades angulares agindo sobre o membro , ou seja:
Sendo assim, voltando a equação da velocidade:
Separando as variáveis por eixo do sistema de referência, obtém-se:
E
Passo 4
Agora, para determinar a aceleração deve-se aplicar a equação:
Similarmente a velocidade angular, a aceleração angular da referência medida a partir do referencial será a soma das acelerações angulares agindo sobre o membro dado por:
Dessa forma, será obtido:
Novamente, separando as variáveis por eixo do sistema de referência, obtém-se:
E: