Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 39
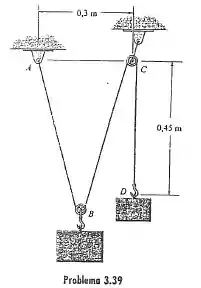
39. Uma “balança” é construída com uma corda de 1,2 m de comprimento e o bloco D de 5 kg. A corda é fixada em um pino em A e passa por duas pequenas polias em B e C. Determine o peso do bloco suspenso em B se o sistema está em equilíbrio.
Passo 1
Falaaa galerinha bonita do RespondeAí, tudo beleza?? Nesse exercício aqui o enunciado nos diz que temos uma balança que construída a partir de uma corda de de comprimento no total, que sustenta dois blocos, e , através de polias como na figura abaixo:
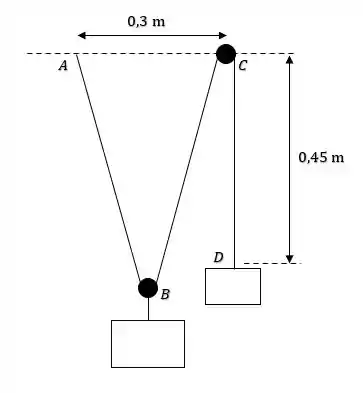
Então se a gente desenhar o diagrama de corpo livre, vamos obter que:
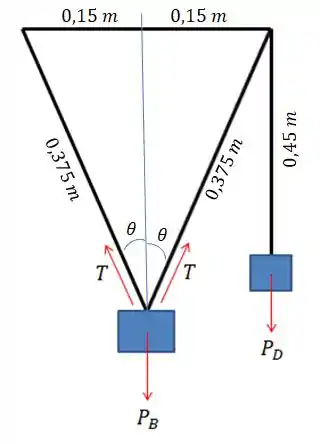
Mas perai, de onde sairam esse ???
Entãããoo... Saca só, como a corda tem , no total, e já foi “gasto” na corda do bloco , vamos ter que:
Agora a gente vai precisar descobrir o valor de pra depois achar o peso do bloco .
Passo 2
Iradoso, então vamos achar a tração. Aqui a gente pode ser malandro e olhar apenas para o bloco :
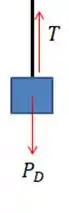
Nessa situação, teremos que a tração que existe na corda é exatamente igual ao peso de , logo podemos igualar as duas coisas, tal que:
Como o enunciado nos deu que , teremos:
Passo 3
Maravilha... Agora vamos fazer desenvolver a equação do equilíbrio no ponto no eixo . Como o sistema está em equilíbrio, teremos que:
Então no ponto , vamos descobrir que:
Mas agora vem a segunda malandragem, porque precisamos encontrar o valor desse cosseno, pra isso podemos primeiro encontrar o valor de seno, dado como:
Então lembrando da relação fundamental entre seno e cosseno, teremos:
Portanto:
Acabamos, heim... Partiu pra próxima???