Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 49
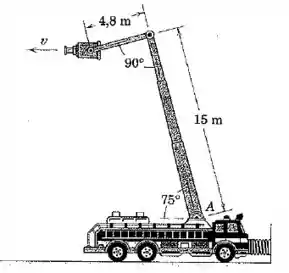
Em um teste de operação de um guindaste móvel de um carro de bombeiros, o equipamento está livre para se mover com seus freios liberados. Na posição apresentada, o caminhão está deformando a mola de rigidez de uma distância de por causa da ação do jato horizontal de água escoando do bocal quando a bomba está ativada. Se o diâmetro de saída do bocal é de , calcule a velocidade do escoamento quando esse deixa o bocal. Determine também o momento adicional que a junção em deve resistir quando a bomba está em operação com o bocal na posição indicada.
Passo 1
Bom, como o caminhão está livre para se mover, a única força que está impulsionando a água para fora é a força vinda da distorção da mola:
E essa força vai gerar uma variação na velocidade de escoamento da água de acordo com:
E a taxa de escoamento de massa também segue uma fórmula simples:
Sendo que é a área do bocal de diâmetro :
E então:
Passo 2
Agora podemos substituir na equação inicial:
E porque a velocidade inicial da água é nula.
Passo 3
Agora queremos saber qual é o momento a que a junção precisa resistir quando o caminhão jorra água na posição indicada no desenho.
Quando a água sai da bomba, podemos imaginar que esta tende a “recuar”, produzindo uma rotação em torno da junção . Em outras palavras: queremos calcular o torque produzido pela água jorrando.
Sabemos que quanto lidamos com escoamento, podemos calcula esse torque da seguinte forma:
E é a o braço de alavanca (cuidado, só pegamos a componente perpendicular à direção da força):
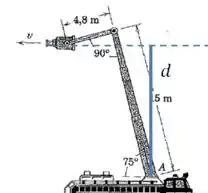
Então, pelo desenho:
E finalmente:
Resposta
A velocidade de escoamento é e o momento é