Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 17

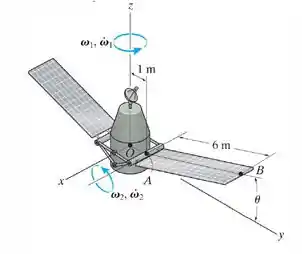
No instante θ = 30 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 29   r a d / s , e tem uma aceleração angular ω ˙ 1 = 5   r a d / s 2 . Simultaneamente, os painéis solares giram com uma velocidade angular constante ω 2 = 5   r a d / s   . Determine a velocidade e aceleração do ponto B localizado na extremidade de um dos painéis solares nesse instante.

Passo 1

O sistema cartesiano rotativo x y z é ajustado paralelamente ao sistema fixo X Y Z , em que a sua origem é o ponto A , conforme mostrado abaixo.

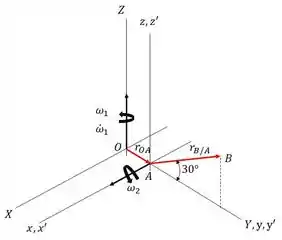
No instante mostrado na figura, o sistema fixo X Y Z coincide com o sistema rotativo x y z . Uma vez que o disco rola sem escorregar, sua velocidade angular ω é sempre direcionada para o eixo y . Logo,

ω = ω 1 = 20 k r a d / s

E

ω ˙ = ω ˙ 1 = 5 k r a d / s 2

Passo 2

Uma vez que o ponto A gira em torno do eixo Z e r O A = 1 j   m , então, a velocidade será

v A = ω 1 × r O A = 20 k × 1 j = - 20 i   m / s

E a aceleração no ponto A é igual a

a A = ω ˙ × r O A + ω × ( ω × r O A )

a A = 5 k × 1 j + 20 k × [ 20 k × ( 1 j ) ]

a A = - 5 i - 400 j   m / s 2

Passo 3

Como mostrado no dcl (passo 1), Para calcular o movimento de B em relação ao ponto A , é necessário estabelecer um sistema rotativo x ' y ' z ' , o qual coincidirá com o sitema x y z no instante considerado. Assim, a velocidade e aceleração de B em relação A serão

( v B / A ) x y z = ( r ˙ B / A ) x y z = [ ( r ˙ B / A ) x ' y ' z ' + ω 2 × ( r B / A ) x ' y ' z ' ]  

( v B / A ) x y z = 0 + 5 i × ( 6 c o s 30 ° j + 6 s e n 30 ° k )

( v B / A ) x y z = - 15 j + 25,98 k m / s

E

( a B / A ) x y z = ( r ¨ B / A ) x y z = [ ( r ¨ B / A ) x ' y ' z ' + ω 2 × ( r ˙ B / A ) x ' y ' z ' ] + ω ˙ 2 × ( r B / A ) x y z + ω 2 × ( r ˙ B / A ) x y z  

( a B / A ) x y z = [ 0 + 0 ] × 0 + ( 5 i ) × ( - 15 j + 25,98 k )

( a B / A ) x y z = - 129,90 j - 75 k m / s 2

Passo 4

Assim, a velocidade e aceleração no ponto B serão iguais a

v B = v A + ω 1 × r B / A + ( v B / A ) x y z

v B = - 20 i + ( 20 k ) × 6 c o s 30 ° j + 6 s e n 30 ° k + - 15 j + 25,98 k

v B = - 124 i - 15 j + 26 k m / s

E

a B = a A + ω ˙ 1 × r B / A + ω 1 × ( ω 1 × r B / A ) + 2 ω 1 × ( v B / A ) x y z + ( a B / A ) x y z

a B = - 5 i - 400 j + ( 5 k ) × 6 c o s 30 ° j + 6 s e n 30 ° k + 20 k × 20 k × 6 c o s 30 ° j + 6 s e n 30 ° k + 2 20 k × - 15 j + 25,98 k + ( - 129,90 j - 75 k )

a B = 569 i - 2608 j - 75 k m / s 2

Resposta

Portanto, a velocidade e a aceleração no ponto B são iguais a - 124 i - 15 j + 26 k m / s e 569 i - 2608 j - 75 k m / s 2   .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um veículo A viaja para o oeste em alta velocidade em uma estrada perfeitamente reta B que é tangente à superfície da Terra no equador. A estrada não possui qualquer curvatura no plano vertical. Deter
Ao contornar uma curva sem inclinação lateral a uma velocidade constante de 25 km/h, o centro C do vagão ferroviário segue uma trajetória circular de raio ρ = 60 m . O eixo longitudinal do vagão perma
Um veiculo experimental A viaja com velocidade constante v em relação à Terra ao longo de uma estrada de ferro ligando norte ao sul. Determine a aceleração de Coriolis a c o r em função da latitude θ
O carro B está contornando a curva com uma velocidade constante de 54 km/h, e o carro A está se aproximando do carro B no cruzamento com uma velocidade constante de 72 km/h. Determine a velocidade que
O disco gira em torno de um eixo fixo através de O com velocidade angular ω = 5 r a d / s e aceleração angular de α = 3r a d / s 2 no instante representado, nos sentidos indicados. O cursor A se deslo