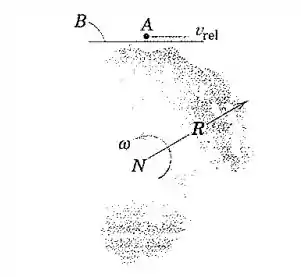
Um veículo A viaja para o oeste em alta velocidade em uma estrada perfeitamente reta B que é tangente à superfície da Terra no equador. A estrada não possui qualquer curvatura no plano vertical. Determine a velocidade necessária do veículo em relação à estrada que dará origem à aceleração nula do veículo na direção vertical. Assuma que o centro da Terra não possui nenhuma aceleração.

Bom galera, nesse exercício vamos precisar buscar o raio e a velocidade de rotação da Terra. Pela tabela D/2, temos que:

Beleza! O enunciado diz que a aceleração resultante na vertical deve ser nula. Vamos desenhar o sistema para entender o que isso quer dizer.

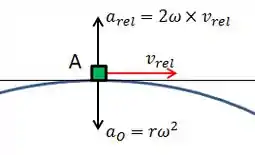
No sistema, existem 2 acelerações: a aceleração que é a aceleração normal da Terra que aponta para o centro devido sua velocidade angular; e a aceleração que é a aceleração de A em relação ao eixo que gira. Para as duas se anularem, temos que:

Encontramos então que: