Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 68
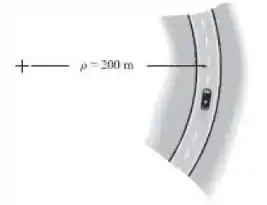
No instante mostrado, o carro de 1500 kg está se movendo com velocidade de 25 m/s, a qual está crescendo a uma taxa de . Determine a intensidade da força de atrito resultante que a estrada exerce sobre os pneus do carro. Despreze a dimensão do carro.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:
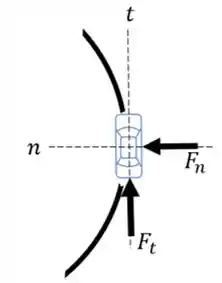
Portanto, o carro está sujeito a força de atrito em duas direções: uma na normal, que está relacionada a componente normal da aceleração, e outra na direção tangencial, que está relacionada ao aumento de velocidade do carro.
Passo 3
Para calcularmos cada uma das componentes das forças, precisamos fazer o somatório das forças em cada uma das direções. Começando pela direção normal, temos:
Já para a componente tangencial, temos:
Passo 4
Por fim, só nos falta calcularmos a intensidade da força de atrito. Utilizando as suas componentes, temos então: