Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 55

Uma placa uniforme tem uma massa de 25 kg. O membro AB está submetido a um momento binário M = 15 N.m e tem uma velocidade angular no sentido horário de 2 rad/s no instante θ = 30 ° . Determine a força desenvolvida no membro CD e a componente tangencial da aceleração do centro de massa da placa nesse instante. Despreze a massa dos membros AB e CD.

Passo 1

Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².

Para começar o exercício, devemos primeiro decompor a aceleração angular em sua componente normal:

a G n = ω 2 r = 2 2 0,45 → a G n = 1,8   m / s 2

Com isso, podemos separar a placa dos membros AB e CD e analisa-la isoladamente conforme a figura a seguir, faremos isso considerando os eixos normal e tangencial e aplicando o somatório de momento em torno do centro de massa da placa:

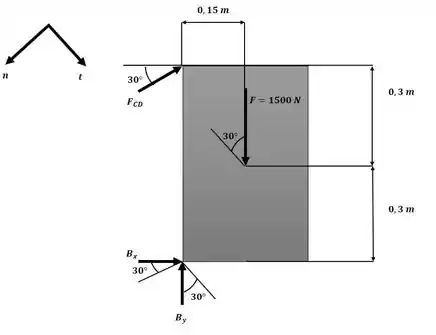
Componente normal:

+ ↙ ∑ F n = m a G n

- F C D - B x c o s 30 ° - B y s e n 30 ° + 25 ( 9,81 ) s e n 30 ° = 25 ( 1,8 )

Essa será nossa equação número 1.

+ ↘ ∑ F t = m a G t

B x s e n 30 ° - B y c o s 30 ° + 25 ( 9,81 ) c o s 30 ° = 25 a G t

Essa será nossa equação número 2.

↺ + ∑ M G = 0

B x 0,3 - B y 0,15 - F C D c o s 30 ° 0,3 - F C D s e n 30 ° 0,15 = 0

Essa será nossa equação número 3.

Passo 2

Conforme proposto no enunciado, a massa do membro AB pode ser desprezada, logo, podemos aplicar um somatório de momento em torno do ponto no membro AB conforme a figura a seguir:

↺ + ∑ M A = 0

B x 0,45 s e n 30 ° - B y 0,45 c o s 30 ° - 15 = 0

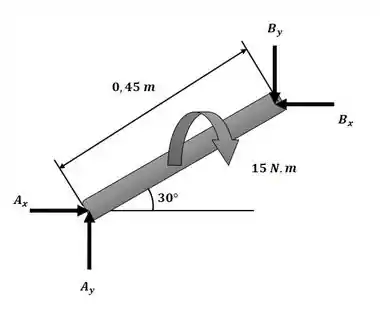
Essa será nossa equação número 4.

Passo 3

Agora, devemos resolver o sistema de equações encontrado, para isso, vamos começar isolando F C D da equação 3 e substituindo na equação 1:

- F C D - B x c o s 30 ° - B y s e n 30 ° + 25 ( 9,81 ) s e n 30 ° = 25 ( 1,8 )

- B x 0,3 0,3348 - B y 0,15 0,3348 - B x c o s 30 ° - B y s e n 30 ° + 25 ( 9,81 ) s e n 30 ° = 25 ( 1,8 )

- 0,896 B x + 0,448 B y - B x c o s 30 ° - B y s e n 30 ° = - 77,625

E, rearranjando, temos:

1,762 B x = - 0,052 B y + 77,625

Essa será nossa equação número 5.

Agora, substituindo esse valor na equação número 4: obtemos o valor de B y :

B x 0,45 s e n 30 ° - B y 0,45 c o s 30 ° - 15 = 0

- 0,052 1,762 B y + 77,625 1,762 0,45 s e n 30 ° - B y 0,45 c o s 30 ° - 15 = 0

B y = - 12,836   N

Substituindo esse valor na equação número 5:

1,762 B x = - 0,052 B y + 77,625

1,762 B x = - 0,052 ( - 12,836 ) + 77,625

B x = 44,434   N

Agora, substituindo o valor de B x e B y na equação 1, temos:

- F C D - B x c o s 30 ° - B y s e n 30 ° + 25 ( 9,81 ) s e n 30 ° = 25 ( 1,8 )

- F C D - 44,434 c o s 30 ° - - 12,836 s e n 30 ° + 25 ( 9,81 ) s e n 30 ° = 25 ( 1,8 )

F C D = 45,56   N

Agora, substituindo os valores de B x e B y na equação 2, podemos obter o valor da aceleração tangencial:

B x s e n 30 ° - B y c o s 30 ° + 25 ( 9,81 ) c o s 30 ° = 25 a G t

( 44,434 ) s e n 30 ° - - 12,836 c o s 30 ° + 25 ( 9,81 ) c o s 30 ° = 25 a G t

a G t = 9,829   m / s 2

Resposta

F C D = 45,56   N

a G t = 9,829   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bobina de 200 kg tem um raio de giração em relação a seu centro de massa k G = 300m m . Se o momento de binário é aplicado à bobina e o coeficiente de atrito cinético entre a bobina e o solo é μ k =
O cilindro de 100 kg rola sem deslizar sobre o plano horizontal. Determine a aceleração de seu centro de massa e sua aceleração angular.
A barra fina uniforme de 60 kg está inicialmente em repouso sobre um plano horizontal liso quando as forças são aplicadas. Determine a aceleração do centro de massa da barra e a aceleração angular da
A barra fina de 12 kg está presa com pino ao rolete pequeno A que desliza livremente ao longo da ranhura. Se a barra é solta do repouso em θ = 0 ° , determine a aceleração angular da barra e a acelera
A esfera de 20 kg rola para baixo sobre o plano inclinado sem deslizar. Determine a aceleração angular da esfera e a aceleração de seu centro de massa.