Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 62
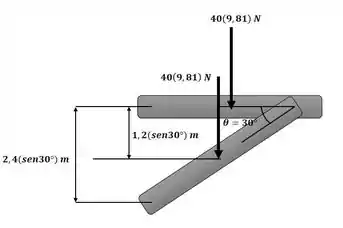
O movimento da porta de garagem uniforme de 40 kg é guiado em suas extremidades pelo trilho. Se a porta é liberada do repouso em = 0°, determine sua velocidade angular no instante = 30°. A mola está originalmente deformada 0,3 m quando a porta é mantida aberta, = 0°. Suponha que a porta possa ser tratada como uma placa fina, e que há um sistema de mola e polia em cada um dos lados da porta.
Passo 1
Iremos considerar a aceleração da gravidade
Vamos considerar também como sendo o comprimento do segmento AC, avaliado a partir do ponto C, e ainda como o comprimento da parte superior do trilho, que vai da polia C até a extremidade da outra polia. Como temos ainda que determinar a velocidade quando = 30°, precisaremos determinar a altura da barra AB nessa posição, que é dada por:
Essa é a variação total . Precisamos ainda encontrar a velocidade linear do centro de massa do segmento AB, que é dado por:
Passo 2
O comprimento total do cabo é dado por:
O termo 2 multiplicando se deve ao fato da geometria do problema, pois o cabo “vai e volta” nessa posição.
Sabemos também que o comprimento do cabo é sempre constante, logo, o que tivermos de variação em um lado, teremos no outro, só que no sentido oposto, logo:
Sabendo que a variação total em A é igual a metade da altura total, conforme visto no passo 1:
Passo 3
Com isso, podemos agora aplicar a equação da conservação da energia mecânica para encontrar velocidade angular da mola no instante = 30° ilustrado na figura a seguir:
