Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 181

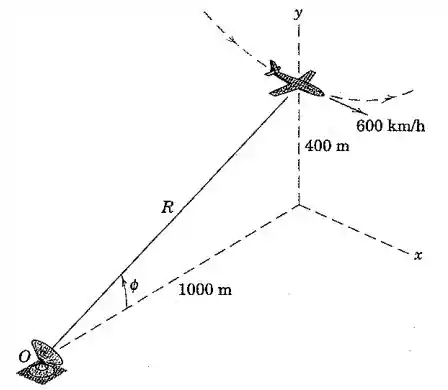
Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo no plano vertical x - y a uma altitude de 400   m , o avião tem uma velocidade de 600   k m / h sem aceleração horizontal x . O raio de curvatura da trajetória na parte inferior é de 1200   m . Para o radar de rastreamento em O , determine os valores registrados de R ¨ e ϕ ¨ para esse instante.

Passo 1

Como o avião está na parte mais baixa da trajetória circular, sua velocidade é totalmente horizontal, ou seja, está na mesma direção do eixo θ . Então:

v R = 0                     v θ = 600   k m / h = 166,7   m / s                   v ϕ = 0

Mas lembre-se de que as componentes da velocidade são dadas assim:

v R = R ˙                     v θ = R θ ˙ cos ⁡ ϕ                     v ϕ = R ϕ ˙

Comparando v R :

R ˙ = 0

Comparando v θ :

R θ ˙ cos ⁡ ϕ = 166,7

Mas pela figura, temos:

R = 1000 2 + 400 2 = 1077   m

ϕ = t g - 1 400 1000 = 21,8 °

Então,

1077   θ ˙ cos ⁡ 21,8 ° = 166,7

θ ˙ = 0,1667   r a d / s

Por último, comparamos v ϕ :

R ϕ ˙ = 0

ϕ ˙ = 0

Passo 2

Como não há aceleração horizontal, a única aceleração é para cima, a aceleração normal do movimento circular:

a = v 2 ρ = 166,7 2 1200 = 23,16   m / s 2

Essa aceleração pode ser decomposta nos eixos R e ϕ :

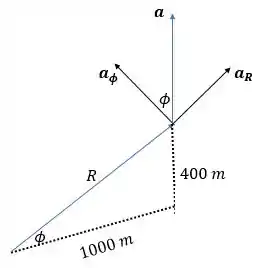
Então, teremos:

a R = a   s e n   ϕ = 23,16   s e n   21,8 ° = 8,601   m / s 2

a ϕ = a cos ⁡ ϕ = 23,16 cos ⁡ 21,8 ° = 21,5   m / s 2

a θ = 0

Passo 3

Show! Agora vamos lembrar que as componentes da aceleração em coordenadas esféricas são dadas assim:

a R = R ¨ - R ϕ ˙ 2 - R θ ˙ 2 cos 2 ⁡ ϕ

a θ = cos ⁡ ϕ R d d t R 2 θ ˙ - 2 R θ ˙ ϕ ˙   s e n   ϕ

a ϕ = 1 R d d t R 2 ϕ ˙ + R θ ˙ 2   s e n   ϕ cos ⁡ ϕ  

Vamos começar comparando em R :

R ¨ - R ϕ ˙ 2 - R θ ˙ 2 cos 2 ⁡ ϕ = 8,601

R ¨ - 1077 0 2 - 1077 0,1667 2 cos 2 ⁡ 21,8 ° = 8,601

R ¨ = 34,4   m / s 2

Agora comparando em ϕ :

1 R d d t R 2 ϕ ˙ + R θ ˙ 2   s e n   ϕ cos ⁡ ϕ = 21,5

Utilizamos a regra do produto para a derivada presente na equação:

1 R 2 R R ˙ ϕ ˙ + R 2 ϕ ¨ + R θ ˙ 2   s e n   ϕ cos ⁡ ϕ = 21,5  

2 R ˙ ϕ ˙ + R ϕ ¨ + R θ ˙ 2   s e n   ϕ cos ⁡ ϕ = 21,5

2 0 0 + 1077   ϕ ¨ + 1077 0,1667 2   s e n   21,8 ° cos ⁡ 21,8 ° = 21,5

ϕ ¨ = 0,01038   r a d / s 2

Resposta

R ¨ = 34,4   m / s 2

ϕ ¨ = 0,01038   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A água escoa continuamente entre duas placas A e B com uma velocidade v de intensidade 30 m/s. O jato é dividido em duas partes por uma placa lisa horizontal C. Sabendo que as vazões em cada uma das c
O jato de água mostrado na figura escoa com uma vazão de 600 L /min e se move a uma velocidade de intensidade de 20 m/s tanto em A quanto em B. O defletor é sustentado por um pino e um suporte em C e
Um jato de ar de alta velocidade sai do bocal A com a velocidade v A e vazão de 0,36 kg/s. O ar colide em um cata-vento causando sua rotação para a posição mostrada na figura. O cata-vento tem uma mas
Uma correia transportadora descarrega carvão à taxa de 120 kg/s. O carvão descarregado é recebido no ponto A de uma segunda correia rolante que o descarrega novamente no ponto B. Sabendo que v 1 = 3 m
14.33. No Problema 14.3, determine o trabalho realizado pela mulher e pelo homem quando cada um mergulha do barco, considerando que a mulher mergulha primeiro.