Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 142

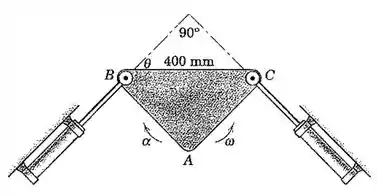
No instante representado, e a placa triangular ABC possui uma velocidade angular no sentido anti-horário de 20 rad/s e uma aceleração angular no sentido horário de 100 rad/s². Determine os módulos da velocidade v e da aceleração a correspondentes da haste do pistão do cilindro hidráulico preso a C.

Passo 1

Bom, primeiro sabemos que o pistão só se movimenta linearmente. Portanto, as velocidades de B e C estarão na direção de seus pistões. Então, podemos representar o mecanismo da seguinte forma:

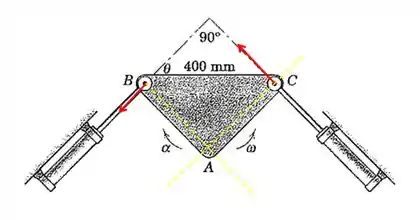
Traçando perpendiculares aos vetores velocidade, encontramos o centro instantâneo no ponto A. Podemos então calcular a velocidade de C.

Passo 2

Agora, vamos usar a equação de aceleração relativa nos pontos C e B:

Sabemos que a componente normal pode ser calculada como:

E ainda que a componente tangencial vale:

Sabendo os módulos e direção destes vetores e sabendo que as acelerações dos pontos B e C estão na direção de seus pistões, podemos esboçar o diagrama completo de vetores aceleração:

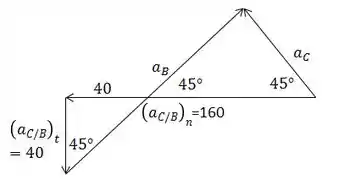
Pelo diagrama, vemos 2 triângulos retângulo com ângulos de 45. Desta formam podemos encontrar a hipotenusa do maior diminuindo 160-40, e consequentemente achar o lado:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 15.14 , resolva o Problema 15.19 2 .

Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante

Um disco com raio de 120m m gira à taxa constante ω 2 = 5r a d / s em relação ao braço A B , que, por sua vez, gira à taxa constante ω 1 = 3r a d / s . Para a posição mostrada na figura, determine a v

A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos

Resolva o Problema 15.228 admitindo que, no instante mostrado na figura, a velocidade angular ω 2 da placa em relação ao braço A E é de 12r a d / s e decresce à taxa de 60r a d / s 2 , enquanto a velo