Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 137

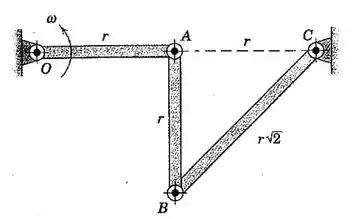
A barra AO possui uma velocidade angular constante   ω no sentido anti-horário durante um curto intervalo de seu movimento. Para a posição mostrada determine as acelerações angulares de AB e BC.

Passo 1

Pessoal, a partir da barra AO, podemos calcular a velocidade e aceleração do ponto A.

v A = r ω   ↑

a A = - r ω 2

Como a barra articulada BC está fixa no ponto C, então a v B   é perpendicular a esta barra.

Agora, analisando o diagrama dos vetores da barra AB, podemos encontrar a velocidade de B:

v B / A = r ω

v B = 2 r ω

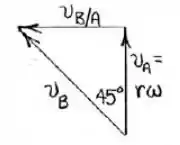
Sabendo v B , podemos encontrar a velocidade angular da barra BC:

v B = ω B C × r B C

ω B C = 2 r ω 2 r = ω

Também podemos encontrar sua aceleração normal e tangencial em relação a BC:

a B n = v B 2 r = 2 r ω 2 ( ↗ 45 ° )

a B t = 0 →   α B C = 0   ( v e r   d i a g r a m a   d e   v e t o r e s   a b a i x o )

Sabendo v B / A , podemos encontrar a velocidade angular da barra AB:

v B A = ω A B × r  

ω A B = ω

Também podemos encontrar sua aceleração normal e tangencial em relação à AB:

a B / A n = r ω 2 ↑    

Passo 2

Neste passo, vamos aplicar a equação da aceleração relativa nos pontos A e B:

a B = a A + a B / A n + a B / A t

Substituindo os resultados encontrados no passo anterior nesta equação, temos:

a B n = a A + a B / A n + a B / A t

2 r ω 2 c o s 45   i ^ + s e n 45   j ^ = - r ω 2 i ^ + r ω 2 j ^ + a B / A t

a B / A t = 2 r ω 2   i ^

Vamos melhor visualizar no diagrama de vetores:

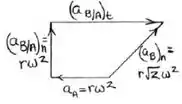
E finalmente calculamos a aceleração angular de AB:

α A B = a B A t r = 2 r ω 2 r = 2 ω 2

Resposta

α B C = 0

α A B = 2 ω 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que, no instante mostrado na figura, a barra AB tem uma velocidade angular constante de 6 rad/s no sentido horário, determine (a) a aceleração angular do membro BDE, (b) a aceleração do ponto
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s e uma aceleração angular de 2 rad/s², ambas no sentido horário, determine a aceleração angu
15.156. Duas barras AE e BD passam por meio de furos usinados em um bloco hexagonal. (Os furos são usinados em planos diferentes para que as barras não se toquem.) Sabendo que, no instante considerado
15.158. Quatro pinos deslizam em quatro ranhuras separadas cortadas em uma placa circular como mostrado na figura. Quando a placa está em repouso, cada pino tem uma velocidade orientada conforme a fig
15.156. Duas barras AE e BD passam por meio de furos usinados em um bloco hexagonal. (Os furos são usinados em planos diferentes para que as barras não se toquem.) Sabendo que, no instante considerado