Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 246
Uma partícula tem as seguintes componentes de posição, velocidade e aceleração: , , , , , . Determine as seguintes grandezas: , , , , , , , , , , , , , , , , , , , , , , , e . Expresse todos os vetores em termos de e , e faça um desenho de todos os vetores em um conjunto de eixos - conforme avança a solução.
Passo 1
Ok, essa é uma questão imensa, então vamos com calma. Primeiro vamos desenhar a situação inicial:
As linhas pontilhadas e indicam as direções tangencial e normal, respectivamente.
Passo 2
Vamos começar com o módulo da velocidade e da aceleração:
E já podemos usar esse resultado para calcular o vetor unitário na direção tangencial. O jeito mais fácil de achar é dividindo a velocidade pelo próprio módulo, porque isso vai dar um vetor unitário na mesma direção:
Passo 3
Agora que temos o vetor unitário na direção tangencial, podemos fazer o produto escalar dele com o vetor da aceleração para encontrar :
Esse é o módulo da aceleração tangencial, para encontrar o vetor é só multiplicar o módulo pelo :
E agora podemos usar esse resultado para achar a outra componente da aceleração:
E agora podemos calcular também o módulo desse vetor:
Passo 4
Agora que temos o módulo da aceleração normal, podemos calcular o raio de curvatura:
E também podemos usar o vetor da aceleração normal para calcular o vetor unitário na direção normal:
Passo 5
Agora vamos pensar em termos de coordenadas polares. Precisamos refazer nosso desenho:
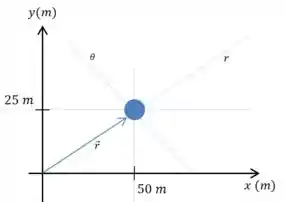
Para encontrar os próximos valores vamos precisar dos vetores unitários nas direções das linhas pontilhadas e :
E o vetor unitário na direção de é simplesmente o rotacionado em no sentido anti-horário:
Agora a componente da velocidade na direção de é simplesmente esse produto interno:
E o vetor é esse módulo multiplicado pelo vetor unitário :
E agora vamos fazer as mesmas contas para a componente na direção de :
Passo 6
Fazendo praticamente as mesmas contas para a aceleração, encontramos o seguinte:
Para a componente na direção de :
E na direção de :
Passo 7
E agora fica faltando encontrar , e :
E a fórmula mais simples que envolve é a da componente da aceleração na direção de :
E a que envolve é a da aceleração na direção de :
Ótimo, finalmente terminamos, agora só falta desenhar alguns dos vetores que ficaram faltando:
E os vetores unitários simplesmente apontam na direção das suas respectivas linhas pontilhadas.
Resposta
; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .
Todas as velocidades estão em , e as acelerações em .