Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 40

Uma partícula se move em órbita bidimensional definida por:

x t = A 2 α t - s e n   α t

y t = A ( 1 - cos ⁡ α t )

  1. Determine a aceleração tangencial at, e a aceleração normal an, como uma função do tempo, onde as componentes tangencial e normal são consideradas em relação à velocidade.
  2. Determine em quais tempos a órbita atingirá seu ponto máximo.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de mecânica Newtoniana.

Para responder ao questionamento do enunciado temos o seguinte diagrama esquemático da problemática apresentada:

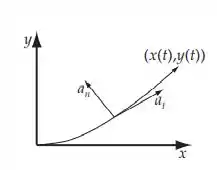
Escrevendo a velocidade como:

v t = v t T t

Teremos que:

a t = d v d t = d v d t T + v d T d t = a t T + a n N

Onde N é o vetor unitário na direção de dT/dt.

Passo 2

Item a

Temos que:

v = x ˙ 2 + y ˙ 2

Resolvendo, teremos:

x ˙ = 2 α A - α A c o s   α t ; e   x ˙ 2 = 4 α 2 A 2 - 4 α 2 A 2 cos ⁡ α t + α 2 A 2 cos 2 ⁡ α t

y ˙ = α A s e n   α t ; e   y ˙ 2 = α 2 A 2 s e n 2   α t

E:

x ˙ 2 + y ˙ 2 = 4 α 2 A 2 - 4 α 2 A 2 cos ⁡ α t + α 2 A 2 cos 2 ⁡ α t + s e n 2   α t = α 2 A 2 4 - 4 cos ⁡ α t + 1 = α 2 A 2 5 - 4 cos ⁡ α t

= > v = α 2 A 2 5 - 4 cos ⁡ α t = α A 5 - 4 cos ⁡ α t

Como a aceleração é a derivada da velocidade, temos:

a t = d v d t = d d t α A 5 - 4 cos ⁡ α t = 2 α 2 A s e n   α t 5 - 4 cos ⁡ α t

Para determinarmos a aceleração normal usamos:

a 2 = a t 2 + a n 2 = > a n = a 2 - a t 2

Onde a é dado por:

a = x ¨ 2 + y ¨ 2

Resolvendo temos:

x ¨ = α 2 A s e n   α t = > x ¨ 2 = α 4 A 2 s e n 2   α t

y ¨ = α 2 A cos ⁡ α t   = > y ¨ 2 = α 4 A 2 cos 2 ⁡ α t

x ¨ 2 + y ¨ 2 = α 4 A 2 s e n 2   α t + cos 2 ⁡ α t = α 4 A 2 = > a = α 2 A

Daí:

a n = a 2 - a t 2 = α 4 A 2 - 2 α 2 A s e n   α t 5 - 4 cos ⁡ α t 2 = A α 2 2 cos ⁡ α t - 1 5 - 4 cos ⁡ α t

Passo 3

Item b

Representando graficamente a aceleração normal, pode-se observar que o ponto de máximo é obtido ao termos:

α t = n π

Sendo:

a n = α 2 A

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Se um projétil se move de forma que sua distância do ponto de lançamento é sempre crescente, encontre o ângulo máximo em relação à horizontal com o qual a partícula poderia ter sido lançada. (Despreze
Uma partícula é lançada com velocidade inicial v 0 para cima de uma rampa que faz um ângulo α com a horizontal. Suponha movimento sem atrito e determine o tempo necessário para que a partícula retorne
Um jogador de softball robusto bate na bola a uma altura de 0,7m acima da base inicial. A bola é liberada do taco do jogador em um ângulo de elevação de 35 ° e se desloca até uma cerca com 2m de altur
Um canhão dispara um projétil de 10k g para o qual as curvas da Figura 2.3 se aplicam. A velocidade na saída da boca do canhão é 140 m s . Qual deverá ser o ângulo de elevação do cano para atingir um
Um projétil é disparado com velocidade v 0 de modo a passar entre dois pontos a uma distância h acima da horizontal. Mostre que, se a arma for ajustada para alcance máximo, a separação entre os pontos