Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 38
Em um jogo de bilhar, a bola se desloca com uma velocidade quando ela atinge as bolas e , que estão em repouso uma ao lado da outra. Considerando as superfícies sem atrito e um choque perfeitamente elástico (ou seja, conservação de energia), determine a velocidade final de cada bola, considerando que a trajetória de é perfeitamente centrada e que atinge e simultaneamente, não é perfeitamente centrada e que atinge um pouco antes de atingir .
Passo 1
Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica. Para determinarmos a velocidade final de cada bola, considerando que a trajetória de é perfeitamente centrada, vamos começar traçando um diagrama para entendermos o problema:
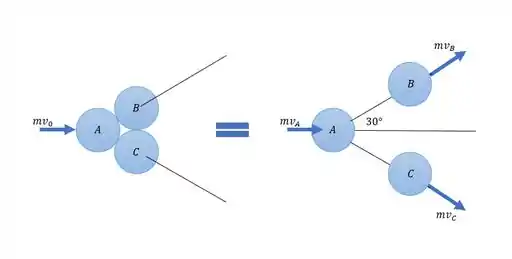
Com isso, durante a colisão, os impulsos de contato fazem ângulos de 30 ° com a velocidade . Assim, podemos determinar a velocidade da bola :
E para a velocidade da bola , temos:
Por simetria, temos que:
Em seguida, por conservação do momento linear, temos que:
Para o eixo , temos:
E para o eixo , temos:
Assim, através da conservação de energia, podemos determinar as velocidades de cada bola. Fica assim:
Agora, que encontramos a velocidade de , vamos determinar as velocidades de e . Encontramos anteriormente que:
Substituindo:
Passo 2
Em seguida, temos a seguinte situação:
A bola tem um primeiro impacto na bola , que passa a estar em movimento com ângulo com a horizontal e velocidade . Logo:
Em seguida, por conservação do momento linear, temos que:
Para o eixo , temos:
E para o eixo , temos:
Assim, através da conservação de energia, podemos determinar as velocidades de cada bola. Fica assim:
Logo, as velocidades vão ser:
Passo 3
Por fim, após a bola impactar a bola , temos:
Em seguida, por conservação do momento linear, temos que:
Para o eixo , temos:
E para o eixo , temos:
Assim, através da conservação de energia, podemos determinar as velocidades de cada bola. Fica assim:
Logo, as velocidades vão ser:
É isso, galerinha. Bora praticar mais pra ficar craque!