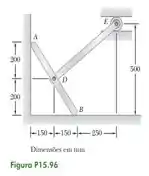
Duas barras de estão conectados pelo pino D mostrado na figura. Sabendo que B se desloca para a esquerda com uma velocidade constante de , determine, no instante mostrado (a) a velocidade angular de cada barra, (b) a velocidade de E.
Passo 1
Bora pra questão 96 agora, meus caros (as)!
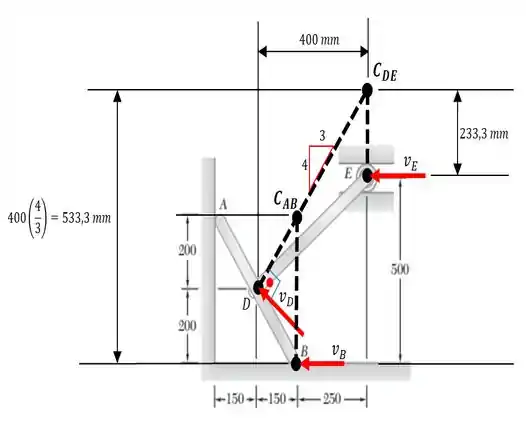
Vamos começar nossa resolução, fazendo um esboço destacando vetorialmente as velocidades e o centro de rotação instantâneo desse sistema ou centros né... Vai que o sistema tem mais do que um. Aqui está, nossa bela imagem...
Passo 2
a) Bom! Inicialmente, a gente tem que determinar a velocidade angular de cada barra. No caso temos duas barras, que são e !
E o nosso sistema vai ter dois centros de rotação instantâneo, que são (relativo à barra ) e ( relativo à barra )!
Bom! A questão nos dá a velocidade com que se desloca para a esquerda, igual à...
Com base na figura anterior, a gente tem que...
Como...
Então, isolando :
No sentido horário, pois é esse o sentido que tende a fazer a barra girar!
Passo 3
Bom! Obtido , podemos obter a velocidade , que será dada por...
, nós podemos obter por semelhança de triângulos...
Sendo assim,
Passo 4
E aí, sim! Obtida , podemos descobrir a velocidade angular da barra !
De acordo com a figura do , temos que...
nós podemos calcular pelo teorema de Pitágoras...
Dessa maneira, isolando e substituindo os valores numéricos...
Obtemos a velocidade angular da barra !
Passo 5
b) Pra finalizar, falta a velocidade em , que chamaremos de !
Pois muito bem! Pela imagem do , temos que...
Como...
Logo, substituindo os valores numéricos...
Pronto! Hasta la vista, baby!
Terminamos aqui!
Resposta
a)
b)