9.4. Localize o centro de gravidade do elemento homogêneo.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
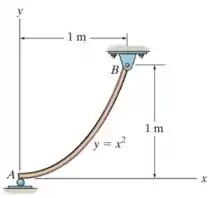
Nesse problema foi dado um elemento homogêneo que segue a curva
Com e dentro do intervalo .
E nosso objetivo é calcular o centro de gravidade desse corpo.
Tem ideia de como fazemos isso?
O centroide de um elemento sem espessura é dado por
Saca só!
Passo 2
Primeiro vamos encontrar qual é o nosso elemento infinitesimal .
Podemos escrever como:
Foi dado na figura que , logo:
Ou seja:
Tranquilo até aqui?
Passo 3
Agora é só calcular as integrais...
Como ...
Continuando...
Substituindo na fórmula de :
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍