Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 4
Determine a massa e localize o centro de massa da barra uniforme. A massa por unidade de comprimento da barra é kg/m.
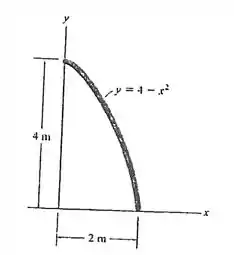
Passo 1
Fala ai galerinha, tudo beleza?
Vamos começar enxergando nosso elemento diferencial, ele é o comprimento do elemento mostrado na figura:
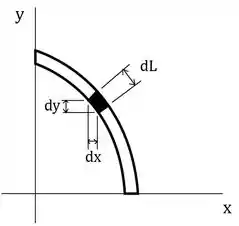
Trazendo isso para nossas coordenadas, usando o bom e velho Pitágoras chegamos em:
Vamos aproveitar e extrair o da raiz:
Olha lá, ficou um ainda dentro, isso tem cara de derivada. Sabendo que , derivando temos então:
Logo, nosso fica:
Passo 2
Para obter o nosso comprimento somaremos todos os pedacinhos elementares da curva através da integral:
Como o percorre o eixo nossos limites de integração irão de a :
Resolvendo essa integral por substituição trigonométrica chegamos em:
Temo a massa por unidade de comprimento da barra, então se multiplicarmos pelo comprimento obteremos a sua massa.
Assim:
Passo 3
Passamos então para o centroide da nossa barra.
Para temos que:
Resolvendo também por substituição trigonométrica:
Agora para :
Mas sabemos que nosso , então:
Resolvendo essa integral temos: