Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 7

Localize o centroide x - da barra circular. Expresse a resposta em termos do raio r e do ângulo de semiarco α .

Passo 1

Show de bola galerinha, o enunciado pede pra gente calcular o centroide x - da barra circular dada como:

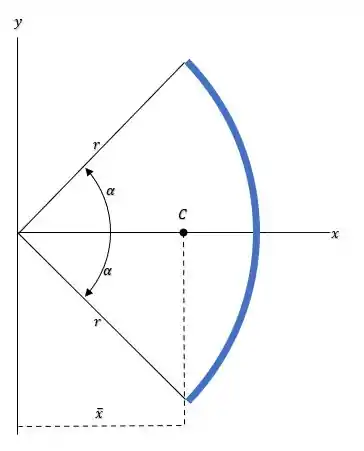
Podemos considerar a barra como sendo uma linha e calcular seu centroide como:

x - = ∫ L x ~ d L ∫ L d L

Belezoca, sabendo disso, bora lá calcular essa posição.

Passo 2

Primeira coisa que precisamos fazer é escrever as coordenadas da barra em função do ângulo α , de modo que:

x = r cos ⁡ α ,     y = r sen ⁡ α

Belezinha, agora podemos calcular d L através da relação:

d L d α = d x d α 2 + d y d α 2

Onde d x d α e d y d α serão dados como:

d x d α = - r sen ⁡ α ,     d y d α = r cos ⁡ α

Logo:

d L d α = - r sen ⁡ α 2 + r cos ⁡ α 2

d L d α = r 2 sen 2 ⁡ α + cos 2 ⁡ α

d L d α = r

Então podemos abusar da notação, e dizer que d L é:

d L = r d α

Passo 3

Iradoso, então vamos ter que a posição x - do centroide será:

x - = ∫ L x ~ d L ∫ L d L = ∫ - α α x   ~ d α ∫ - α α d α

Onde x   ~ a gente já havia expressado como:

x   ~ = r cos ⁡ α

Isso quer dizer que:

x - = ∫ - α α r cos ⁡ α d α ∫ - α α d α

Portanto:

x - = r sen ⁡ α - r sen ⁡ - α α - - α

x - = 2 r sen ⁡ α 2 α

x - = r sen ⁡ α α

Resposta

x - = r sin ⁡ α α

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o centroide da área a seguir:
Determine a b para que x - = y - :
Calcule o centroide da área a seguir:
Um arame homogêneo e fino é dobrado na forma do perímetro a seguir. Calcule o seu centro de gravidade.
Um arame homogêneo e fino é dobrado na forma do perímetro a seguir. Calcule o seu centro de gravidade.