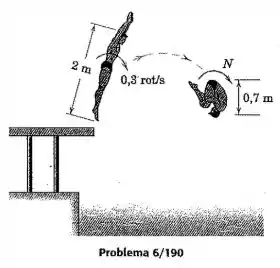
Logo após deixar a plataforma, o corpo do atleta de de saltos ornamentais, completamente estendido, possui uma velocidade de rotação de em relação a um eixo normal ao plano da trajetória. Estime a velocidade durante o salto, quando o atleta tiver assumido a posição grupada. Proponha hipóteses razoáveis em relação ao momento de inércia de massa do corpo em cada configuração.

Pela conservação da quantidade de movimento angular, temos

Para resolvermos em termos da quantidade de movimento angular, devemos aproximar a geometria do corpo do atleta em cada uma das configurações por uma geometria cuja equação de momento de inércia de massa seja conhecida.

Nesta altura do campeonato, você já deve ter notado o quão necessário é saber as equações de momento de inércia para as principais figuras geométricas. Mas não precisa se desesperar, qualquer coisa é só voltar um pouco e assistir nossa aula sobre momento de inércia!

Retomando o problema, aproximaremos o corpo do atleta como uma barra esbelta na configuração 1 e como uma esfera na configuração 2.