Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 149
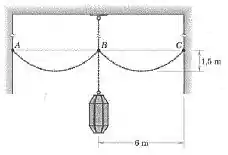
Uma luminária está suspensa do teto de um pórtico externo. Quatro correntes, duas das quais estão mostradas, previnem movimento excessivo da luminária devido ao vento. Se as correntes pesam 200 N por metro de comprimento, determine a força trativa na corrente em C e o comprimento L da corrente BC.
Passo 1
Primeiro vamos anotar as informações que a questão e a imagem nos oferecem, para facilitar a visualização:
Estas informações podem ser visualizadas abaixo
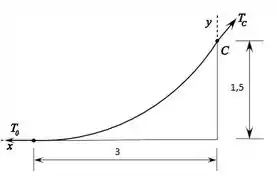
Agora, vamos lembrar a equação da curva formada pelo cabo abaixo:
Ou,
Também, temos que:
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira, temos:
Resolvendo a equação acima, teremos que:
Logo,
Como,
Então,
Passo 3
Para encontrarmos os comprimentos L da corrente BC, temos que lembrar da equação:
Sabendo disso, basta substituir os valores, portanto:
Como esse comprimento é somete metade do que queremos, então: