Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 200
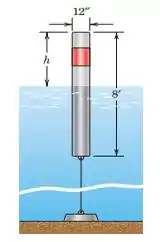
Uma bóia de marcação de canal consiste em uma cavidade de 8 pés cilindro de aço de 12 pol. de diâmetro pesando 180 libras e ancorado na parte inferior com um cabo, conforme mostrado. Se na maré alta, calcule a tensão T em o cabo. Encontre também o valor de h quando o cabo diminui quando a mar é desce. O peso específico de a água do mar é . Suponha que a bóia seja pesada em sua base para que permaneça vertical.
Passo 1
E ai gurizada tudo belezinha???
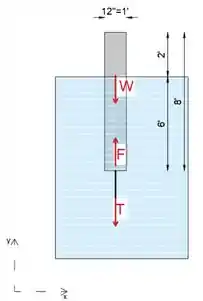
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da bóia com seu peso, tensão do cabo e força de flutuabilidade atuando sobre ele.
A força de empuxo é igual ao produto do peso e volume específicos da água.
O volume do cilindro debaixo d'água é:
Substitua V e por seus valores na expressão de F.
Passo 2
Equacionando a soma das forças na direção y a zero, podemos determinar a tensão no cabo.
A partir daqui, podemos expressar T como:
Substitua F e W por seus valores.
Passo 3
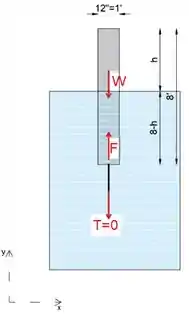
Para a segunda parte do problema, vamos isolar e desenhar o diagrama de corpo livre do anexo que é igual a zero.
A força de empuxo é igual ao produto do peso e volume específicos da água.
O volume do cilindro debaixo d'água é:
Substitua V e por seus valores na expressão de F.
Passo 4
Ao igualar a soma das forças na direção y a zero, obteremos a equação em que a altura h é a única incógnita.
Substitua F e W por seus valores.
A partir daqui, podemos expressar h como: