Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 05

A magnitude da força P é aumentada lentamente. A caixa homogênea de massa m desliza ou tomba primeiro? Indique o valor de P que causaria cada ocorrência. Negligencie qualquer efeito do tamanho dos pés pequenos.

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar se com o aumento gradual da força P , a caixa de massa m irá tombar ou deslizar primeiro e qual o valor de P que causa esse movimento.

Então bora resolver! Vamos começar analisando o diagrama de corpo livre para o item a .

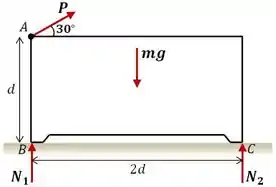
Para o caso de deslizamento, a resistência ao atrito corresponde à componente horizontal da força P aplicada, logo:

μ s N 1 + N 2 = P cos ⁡ 30 °

Onde N 1 e N 2 são as reações normais da superfície na caixa nos apoios em A e C , respectivamente.

Passo 2

Até aqui tranquilo né? Mas nós ainda não definimos as reações N 1 e N 2 para determinar P . Para isso, sabendo que o corpo está em equilíbrio, podemos utilizar o somatório de momentos em torno do ponto A para determinar N 2 e, posteriormente, o somatório de forças na direção y para determinar N 1 . Então bora lá!

∑ M A = 0

N 2 * 2 d - P cos ⁡ 30 ° * d - m g * 2 d 2 = 0

N 2 = P cos ⁡ 30 ° * d + m g * d 2 d

N 2 = P cos ⁡ 30 ° 2 + m g 2

∑ F y = 0

N 1 + N 2 + P sen ⁡ 30 ° - m g = 0

N 1 = m g - P cos ⁡ 30 ° 2 - m g 2 - P sen ⁡ 30 °

N 1 = m g 2 - P cos ⁡ 30 ° 2 - P sen ⁡ 30 °

Passo 3

Por fim, para encontrar P é só substituir esses resultados de N 1 e N 2 na equação do Passo 1:

μ s m g 2 - P cos ⁡ 30 ° 2 - P sen ⁡ 30 ° + P cos ⁡ 30 ° 2 + m g 2 = P cos ⁡ 30 °

μ s m g - P sen ⁡ 30 ° = P cos ⁡ 30 °

Para μ s = 0,5 :

0,5 m g - P sen ⁡ 30 ° = P cos ⁡ 30 °

2 P cos ⁡ 30 ° + P sen ⁡ 30 ° = m g

P = m g 2 cos ⁡ 30 ° + sen ⁡ 30 °

P = 0,448 m g

Passo 4

Até aqui definimos P para a condição de deslizamento. Agora precisamos analisar P para o caso que a caixa tomba e comparar os dois casos. Para o caso de tombamento, a caixa perde o contato no apoio em A , logo a reação normal à superfície nesse ponto é nula:

N 1 = 0

Assim como no caso anterior, podemos fazer o equilíbrio de momentos em torno de A para determinar N 2 e, posteriormente, o equilíbrio de forças na direção y para determinar P .

∑ M A = 0

N 2 * 2 d - P cos ⁡ 30 ° * d - m g * 2 d 2 = 0

N 2 = P cos ⁡ 30 ° * d + m g * d 2 d

N 2 = P cos ⁡ 30 ° 2 + m g 2

∑ F y = 0

N 2 + P sen ⁡ 30 ° - m g = 0

P cos ⁡ 30 ° 2 + m g 2 + P sen ⁡ 30 ° - m g = 0

P cos ⁡ 30 ° + m g + 2 P sen ⁡ 30 ° - 2 m g = 0

P cos ⁡ 30 ° + 2 sen ⁡ 30 ° = m g

P = m g cos ⁡ 30 ° + 2 sen ⁡ 30 °

P = 0,536 m g

Passo 5

Show de bola! Como já temos P para os casos de deslizamento e tombamento, podemos compara-los para descobrir qual das duas situações ocorre primeiro com o aumento gradual de P :

P d e s l i z a m e n t o = 0,448 m g < P t o m b a m e n t o = 0,536 m g

Portanto, ocorre primeiro o deslizamento da caixa e:

Ufa! Essa já foi hein? Partiu pra próxima!

HYPERLINK "https://emojiterra.com/pt/rosto-piscando/"

Resposta

P d e s l i z a m e n t o = 0,448 m g

P t o m b a m e n t o = 0,536 m g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/18) A barra uniforme A B de massa m e comprimento l está apoiada contra a parede vertical como mostrado . O coeficiente de atrito estático entre as superfícies de apoio e as extremidades da barra é
6/34) Dois automóveis , ambos tendo o centro de massa localizado como mostrado , a meia distância entre os eixos traseiro e dianteiro , são idênticos exceto que um tem tração dianteira e o outro tem t
6/32) O rolo de papel deve ser girado lentamente para cima da rampa por uma força trativa T aplicada ao papel , à medida que ele é desenrolado horizontalmente . O coeficiente de atrito entre o rolo e
6/35) O cilindro sólido de 10k g está em repouso no bloco em V inclinado . Se o coeficiente de atrito estático entre o cilindro e o bloco vale 0,50 , determine (a) a força de atrito F atuando sobre ca
6/33) Assumindo que o trabalhador seja forte o suficiente , será possível manter o equilíbrio da prancha uniforme de 7m na posição mostrada , exercendo uma força horizontal na corda ? O coeficiente de