Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 143

Em um dado instante, a barra AB tem os movimentos angulares mostrados. Determine a velocidade angular e a aceleração angular da barra CD nesse instante. Há um anel em C.

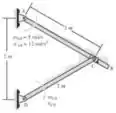
Passo 1

A origem dos eixos coordenados, seja ele o referencial ou o fixo, iremos considerar como tendo sua origem no ponto A, como a mostra a figura abaixo.

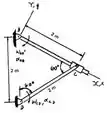
Além disso, vamos escrever o que o enunciado nos fornece (e também com base na figura).

v A = 0

a A = 0

Ω = - 5 k   r a d / s

Ω ˙ = - 12 k   r a d / s 2

r C / A = 2 i   m

v C / A x y z = v C / A x y z i

a C / A x y z = a C / A x y z i

Passo 2

Calcularemos v C , com isso:

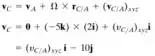
Mas v C também pode ser calculado por v C = ω C D × r C D , então, podemos substituir essa equação com seus respectivos valores na equação acima. Então:

v C / A x y z i - 10 j = - ω C D k × ( 2 cos ⁡ 60 ° i + 2 sen ⁡ 60 ° j )

v C / A x y z i - 10 j = 1.732 ω C D i - ω C D j

Resolvendo a equação em i e j, teremos:

ω C D = 10   r a d / s

v C / A x y z = 1.732 10 = 17.32   r a d / s 2

Passo 3

Bom, calculamos os valores acima, agora podemos fazer o cálculo de α C D . Para isso, iremos utilizar a fórmula abaixo.

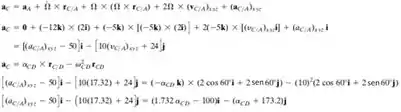
Resolvendo nas coordenadas i e j, teremos:

- 10 17.32 + 24 = - α C D + 173.2 ∴ α C D = 24     r a d / s 2

a C / A x y z - 50 = 1.732 24 - 100 ∴ a C / A x y z = - 8.43   m / s 2

Resposta

ω C D = 10   r a d / s

α C D = 24   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro hidráulico está se estendendo com a velocidade e aceleração mostradas. Determine a aceleração angular da manivela AB e do segmento BC no instante mostrado.
O disco rola sem deslizar e, em um dado instante, tem o movimento angular mostrado. Determine a velocidade angular e a aceleração angular do membro com ranhura BC nesse instante. O pino em A está fixo
No instante mostrado, o barco A se desloca com uma velocidade de 15 m/s, que está diminuindo a 3 m/s², enquanto o barco B se desloca com uma velocidade de 10 m/s, que está aumentando a 2 m/s². Determi
A engrenagem tem o movimento angular mostrado. Determine a velocidade angular e a aceleração angular do membro com ranhura BC nesse instante. O pino A está fixo à engrenagem.
A água deixa o impulsor da bomba centrífuga com uma velocidade de 25 m/s e aceleração de 30 m/s², ambas medidas em relação ao impulsor ao longo da linha da pá AB. Determine a velocidade e a aceleração