Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 147

O mecanismo de dois membros serve para amplificar o movimento angular. O membro AB tem um pino em B que está confinado a se deslocar dentro da ranhura do membro CD. Se, no instante mostrado, AB (entrada) tem uma velocidade angular ω A B = 2,5   r a d / s e uma aceleração angular α A B = 3   r a d / s 2 , determine a velocidade angular e a aceleração angular de CD (saída) nesse instante.

Passo 1

Começaremos o exercício definindo nosso eixo xyz de referência conforme a figura a seguir, que também será utilizada nos passos posteriores para escrever as equações de velocidade e acelaração:

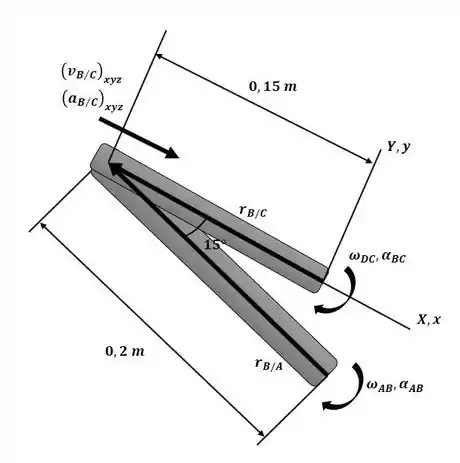
Com base no diagrama, podemos extrair algumas informações:

v → C = a → C = 0

Ω = - ω D C k →

Ω ˙ = - α B C k →

r → B / C = - 0,15 i →   m

v → B / C x y z = v B / C x y z i →

a → B / C x y z = a B / C x y z i →

Passo 2

Agora iremos encontrar a velocidade do ponto B:

v → B = ω A B × r → B / A = - 2,5 k → × ( - 0,2 c o s 15 ° i → + 0,2 s e n 15 ° j → )

v → B = 0,1294 i → + 0,483 j →   m / s

Agora podemos aplicar a equação da aceleração com relação aos pontos A e B:

a → B = α A B × r → B / A - ω A B 2 r → B / A

a → B = - 3 k → × - 0,2 c o s 15 ° i → + 0,2 s e n 15 ° j → - 2,5 2 ( - 0,2 c o s 15 ° i → + 0,2 s e n 15 ° j → )

a → B = 1,3627 i → + 0,256 j →   m / s 2

Agora iremos aplicar a equação da velocidade relativa com relação aos pontos B e C:

v → B = v → C + Ω × r → B C + v → B / C x y z

0,1294 i → + 0,483 j → = 0 + - ω D C k → × - 0,15 i → + v B / C x y z i →

0,1294 i → + 0,483 j → = v B / C x y z i → + 0,15 ω D C i →

Igualando as componentes i e j, temos:

v B / C x y z = 0,1294   m / s

ω D C = 3,22   r a d / s

Passo 3

Agora podemos aplicar a equação da aceleração relativa para o sistema:

a → B = a → C + Ω   ˙ × r → B / C + Ω × Ω × r → B / C + 2 Ω × v B / C x y z + a B / C x y z

1,3627 i → + 0,256 j → = 0 + - α C D k → × - 0,15 i → + - 3,22 k → × - 3,22 k → × - 0,15 i → + 2 - 3,22 k → × 0,1294 i → + a B / C x y z i →

1,3627 i → + 0,256 j → = 1,555 + a B / C x y z i → + ( 0,15 α D C - 0,833 ) j →

Igualando a componente j, temos:

0,256 = 0,15 α D C - 0,833 → α D C = 7,26   r a d / s 2

Resposta

ω D C = 3,22   r a d / s

α D C = 7,26   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o problema 15. 255, assumindo que θ = 90 ∘ 15.255 - A haste BC de 24 pol de comprimento é conectada por articulações esféricas a um braço rotativo AB e a um colar C que desliza na haste fixa D
A manivela AB tem uma velocidade angular constante de 1,5 rad / s no sentido anti-horário. Para a posição mostrada, determine (a) a aceleração angular da haste BD, (b) a aceleração do colar D.
Uma corrente é enrolada em torno de duas engrenagens de 40m m de raio, que podem girar livremente em relação ao braço A B , de 320m m . A corrente move-se em torno do braço AB no sentido horário a uma
Uma corrente é enrolada em torno de duas engrenagens de 40m m de raio, que podem girar livremente em relação ao braço A B , de 320m m . A corrente move-se em torno do braço AB no sentido horário a uma
O braço AB tem uma velocidade angular constante de 16 rad / s no sentido anti-horário. No instante em que θ = 90 ∘ , determine a aceleração (a) do colar D, (b) do ponto médio G da barra BD.