Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 102
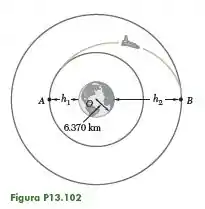
A melhor maneira de transferir um veículo espacial de uma órbita circular mais interna para uma outra órbita coplanar mais externa é acionando seus motores quando ele passar por , a fim de aumentar sua velocidade e pô-lo em uma órbita elíptica de transferência. Um outro aumento de velocidade quando ele passar por irá colocá-lo na órbita circular desejada. Para um veículo em uma órbita circular em torno da Terra a uma altitude que deve ser transferido para uma órbita circular a uma altitude , determine (a) o aumento de velocidade requerido em e , (b) a energia total por unidade de massa necessária para executar a transferência.
Passo 1
Oi, galerinha! Beleza? Vamos à resolução do problema!!
O enunciado e a figura nos fornecem como dados:
Nosso dever é determinar o aumento de velocidade requerido em e e a energia total por unidade de massa necessária para executar a transferência do veículo de uma órbita circular mais interna para uma outra órbita coplanar mais externa. Como temos as altitudes dos pontos e e o raio da Terra, vamos incialmente calcular e .
Aplicando o princípio da conservação do momento angular:
Passo 2
Calculando a energia cinética e potencial.
Ponto A:
Aplicando agora a Eq. 13.17, usada para a energia potencial quando a variação da força da gravidade não pode ser desprezada:
No caso de um corpo de massa sujeito à atração gravitacional da Terra, o produto , pode ser expresso de acordo a Eq. (12.29),
Sabemos que,
e
Então, substituindo na Eq. (12.29), temos,
Substituindo em :
Ponto B:
Aplicamos a Eq. 13.17 para obter a energia potencial:
Passo 3
Em posse das energias cinética e potencial, vamos aplicar o princípio da conservação da energia:
Sabemos que
Então,
Passo 4
O valor da velocidade inicial correspondente a uma órbita circular é encontrado através da Eq. 12.44:
Ponto A:
Ponto A:
Passo 5
Vamos então encontrar:
Aumento de velocidade requerida em , :
Aumento de velocidade requerida em , :
Passo 6
E, por fim, a energia total por unidade de massa.