Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 76
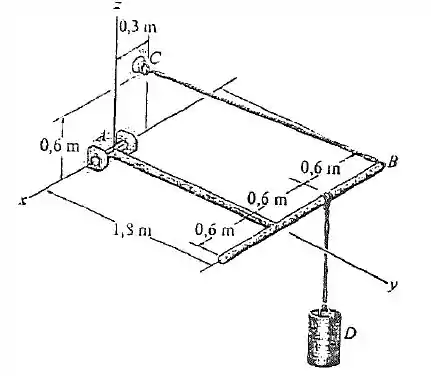
76. O membro é sustentado por um pino em e um cabo . Se a carga em é de , determine as componentes da reação no pino e a tração no cabo .
Passo 1
Fala, querido! Queremos as reações no pino e no cabo.
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso é um cabo e um pino, segundo a tabela do capítulo , seção , esse tipo de conexão por cabo só exerce uma força ou tração na direção do cabo, o pino exerce reação nas três direções dos eixos coordenados e reação ao momento em dois eixos, no nosso caso, esses eixos serão e .
Abaixo temos um diagrama de corpo livre que vai nos ajudar a ver o que está acontecendo.
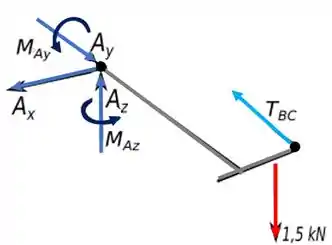
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.
O macete é sempre começar com as equações que te oferecem menos incógnitas.
Passo 2
Para determinar a tração no cabo nessa situação, será melhor expressá-la na forma vetorial, nessa forma teremos as componentes da tração do cabo, podendo assim usar as equações de equilíbrio para cada direção com a componente adequada da tração.
Para expressar essa força de tração, precisamos achar o vetor unitário que tem mesma direção e sentido que a força de tração. Percebe que podemos usar um vetor que sai de e vai para .
Para achar um vetor nessa direção, podemos fazer ponto final menos inicial
Aí o vetor unitário pode ser encontrado da seguinte maneira:
Assim no nosso caso temos que o vetor unitário de é:
Agora que temos o vetor unitário, vamos expressar a tração da corda . O que a gente faz é multiplicar o módulo da força pelo vetor unitário na direção da força.
Daí tiramos
Passo 3
Vamos analisar primeiro a equação de equilíbrio referente ao momento em relação ao eixo , que é o que oferece somente uma incógnita. Vamos usar o sentido anti-horário do eixo como positivo (segundo a regra da mão direita).
Percebe que aqui somente a componente da tensão gera momento em relação a . Isso porque a componente em está dentro do eixo de rotação e a componente tem sua linha de ação passando por .
Passo 4
Agora que temos o valor de vamos avaliar a equação de equilíbrio do momento em relação aos outros eixos para acharmos os momentos de reação exercidos pelo pino. Vamos usar o sentido anti-horário do eixo como positivo.
Como tem sua linha de ação passando por e é paralela a , elas não geram momento aqui.
Agora olhando para o eixo . Vamos usar o sentido anti-horário do eixo 𝑧 como positivo.
Passo 5
Agora vamos analisar as equações de equilíbrio referente a força, para cada direção.
Para :
Por fim, para :