Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 27
O sistema é liberado a partir do repouso com o cabo esticado. Para os coeficientes de atrito e , calcule a aceleração de cada corpo e a tração no cabo. Despreze a pequena massa e o atrito nas polias.
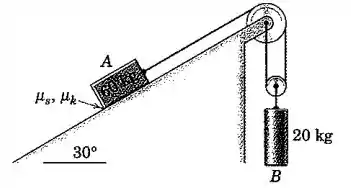
Passo 1
Vamos primeiramente testar se é possível haver equilíbrio estático no sistema. Para o bloco , teríamos:
Para o bloco , sendo a força de atrito, teríamos:
Ou seja, precisaríamos de uma força de atrito de módulo no sentido subindo o plano inclinado para equilibrar as forças do sistema. Porém, o módulo da força de atrito estático máxima é:
Ou seja, a força de atrito não seria capaz de equilibrar o sistema. Sendo assim, há movimento no sistema e passamos a considerar a força de atrito dinâmico:
orientada no sentido oposto ao do movimento, ou seja, ela empurra o bloco morro acima.
Passo 2
Agora vamos aplicar a Segunda Lei de Newton ao bloco :
Também aplicamos a Segunda Lei de Newton ao bloco :
Passo 3
Por enquanto, chegamos a duas equações, mas com três incógnitas, a saber: , e . O que falta é a equação que relaciona a aceleração dos dois blocos:
Agora sim temos três equações e três incógnitas, e podemos resolver o sistema:
cuja solução é:
O sinal positivo de significa que ela está no sentido de descer a inclinação, e o sinal positivo de significa que a aceleração é para cima.
Resposta
descendo a inclinação
para cima