Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 168

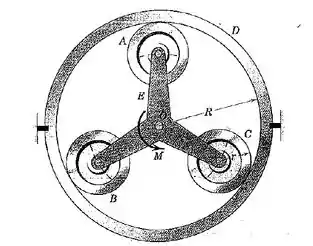
Um sistema de engrenagens planetárias é apresentado, onde os dentes das engrenagens são omitidos da figura. Cada uma das três engrenagens planetárias idênticas A , B e C tem uma massa de 0,8   k g , um raio r = 50   m m , e um raio de giração de 30   m m em relação ao seu centro. O suporte E tem uma massa de 1,2   k g e um raio de giração em relação a O de 60   m m . A engrenagem anular D tem um raio R = 150   m m e é fixa. Se um torque M = 5   N . m é aplicado ao eixo do suporte das planetárias em O , determine a aceleração angular inicial α do suporte.

Passo 1

Os deslocamentos linear infinitesimal e angular infinitesimal podem ser obtidos por

d S P = R - r d θ

d θ A = d S P r = R r - 1 d θ

Da mesma forma que a velocidade linear e angular em P são determinadas por

v P = R - r θ ˙

ω = v P r = R r - 1 θ ˙

E também as acelerações serão:

a P t = R - r α

α A = a P t r = R r - 1 α

Passo 2

Assim, a energia cinética do suporte será determinada por

d T s u p = d 1 2 I o ω 2 = I o ω d ω = I o α d θ

Por outro lado, a energia cinética das engrenagens será

d T e n g = 3 d 1 2 I A ω A 2 + d 1 2 m A v P 2

d T e n g = 3 1 2 I A 2 ω d ω + 1 2 m A 2 v P d v P

d T e n g = 3 I A α A d θ A + m A a P t d S P

d T e n g = 3 I A R r - 1 2 α d θ + m A R - r 2 α d θ

d T e n g = 3 R - r 2 I A r 2 + m A α d θ

Passo 3

Logo, o trabalho total será a soma das energias cinéticas:

d U = d T s u p + d T e n g

Uma vez que

d U = M d θ

Temos:

M d θ = I O + 3 R - r 2 I A r 2 + m A α d θ

M = I O + 3 R - r 2 I A r 2 + m A α

α = M I O + 3 R - r 2 I A r 2 + m A

α = 5 1,2 0,06 2 + 3 0,15 - 0,05 2 0,8 0,03 2 0,05 2 + 0,8

Portanto,

α = 135,3   r a d / s 2

Resposta

A aceleração angular inicial α do suporte é igual a 135,3   r a d / s 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo do repouso, uma pedra de 1 kg cai de uma altura h e bate no chão com uma velocidade de 15 m / s . (a) Encontre a energia cinética da pedra quando ela bate no chão e a altura h da queda. (b) R
Um satélite de 450 kg é posto em uma órbita circular a 6.360 km acima da superfície da Terra. Nessa elevação, a aceleração da gravidade é de 2,4 m/ s 2 . Determine a energia cinética do satélite, sabe
Em uma operação de mineração, uma caçamba cheia de minério é suspensa por um guindaste móvel que se desloca lentamente ao longo de uma ponte estacionária. O guindaste desloca-se a uma velocidade de 3
Em uma operação de mineração, uma caçamba cheia de minério é suspensa por um guindaste móvel que se desloca lentamente ao longo de uma ponte estacionária. A caçamba não deverá oscilar mais que 4 m hor
Determine a máxima velocidade escalar teórica que pode ser alcançada em uma distância de 360 m por um carro inicialmente em repouso considerando que não há deslizamento. O coeficiente de atrito estáti