Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 42

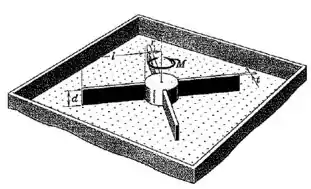
Uma mesa de ar é usada para estudar o movimento elástico de modelos flexíveis de espaçonaves. O ar pressurizado que escapa de numerosos furos pequenos na supefície horizontal fornece um colchão de ar para sustentação que elimina grande parte do atrito. O modelo apresentado é constituído por um núcleo cilíndrico de raio r e quatro hastes de comprimento l e pequena espessura t . O cilindro e as quatro hastes, todos têm a mesma profundidade d e são construídos do mesmo material com massa específica ρ . Suponha que a espaçonave é rígida e determine o momento M que deve ser aplicado ao cilindro para girar o modelo a partir do repouso até uma velocidade angular ω em um período de tempo de τ segundos. (Note que para uma espaçonave com hastes muito flexíveis, o momento deve ser criteriosamente aplicado ao cilindro rígido para evitar grandes deflexões elásticas indesejáveis das hastes.)

Passo 1

Primeiro vamos encontrar uma expressão que dê a aceleração angular necessária para acelerar o sistema até uma velocidade angular ω em um tempo τ a partir do repouso:

ω = α τ

α = ω τ

E para gerar essa aceleração angular, o momento necessário é:

M = I α

M = I ω τ

Ou seja, nosso problema é calcular o momendo de inércia do sistema, pois já temos todas as outras variáveis.

Passo 2

Vamos pensar no momento de inércia de uma única haste. Em relação ao próprio centro de massa da haste, o momendo seria:

I C M = 1 12 M L 2

Mas queremos o momento de inércia em relação ao centro do sistema. Então pelo teorema dos eixos paralelos:

I O = I C M + M d 2

Onde d é a distância entre o centro de massa das hastes e o centro do sistema:

d = 1 2 L + r

Onde r é o raio do cilindro que fica no centro da hélice. Por isso o momento de inércia de cada haste é:

I H é l i c e = 1 12 M L 2 + M L 2 + r 2

E o momento de inércia do cilindro no centro do sistema é:

I c i l i n d r o = 1 2 M c r 2

Então o momento de inércia total do sistema é:

I T = I c i l i n d r o + 4 I H é l i c e

I T = 1 2 M c r 2 + 12 1 4 M L 2 + M L 2 + r 2

Passo 3

Agora precisamos encontrar expressões para as massas em função da massa específica ρ .

Começando pela massa do cilindro:

M C = ρ V C

M C = ρ π r 2 d

E agora a massad e cada haste:

M H = ρ V H

M H = ρ L d t

Vamos substituir isso na expressão do momento de inércia e simplificar um pouco:

I T = 1 2 ρ π r 2 d r 2 + 4 1 12 ρ L d t L 2 + ρ L d t L 2 + r 2

I T = 1 2 ρ π d r 4 + 4 ρ L d t L 2 12 + L 2 4 + L r + r 2

I T = 1 2 ρ π d r 4 + 4 ρ L d t L 2 3 + L r + r 2

I T = ρ d 1 2 π r 4 + 4 L t 1 3 L 2 + L r + r 2

Agora vamos voltar para a fórmula que escrevemos lá em cima:

M = I ω τ

M = ω ρ d τ 1 2 π r 4 + 4 L t 1 3 L 2 + L r + r 2

Resposta

O momento necessário é M = ω ρ d τ 1 2 π r 4 + 4 L t 1 3 L 2 + L r + r 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tambor de 100 mm de raio está preso a um disco de 200 mm de raio. O disco e o tambor têm peso combinado de 50 N e um raio de giração combinado de 150 mm. Uma corda é presa como mostra a figura e pu
Uma barra de massa m é mantida, como mostra a figura, entre quatro discos, cada um de massa m' raio r = 75 mm. Determine a aceleração da barra imediatamente depois dela ter sido liberada do repouso, s
A engrenagem C tem uma massa de 5 kg e um raio de giração do centro de massa de 75 mm. Uma barra uniforme AB tem uma massa de 3 kg e a engrenagem D é fixa. Se o sistema é liberado do repouso na posiçã
O centro de gravidade G de uma roda desbalanceada de 1,5 kg está localizado a uma distância r = 18 mm de seu centro geométrico B. O raio da roda é R = 60 mm e seu raio de giração em relação ao centro
As extremidades da haste uniforme AB de 2 kg são presas a cursores de peso desprezível que deslizam sem atrito ao longo de hastes fixas mostradas na figura. A haste AB está em repouso na posição θ = 2