Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 109

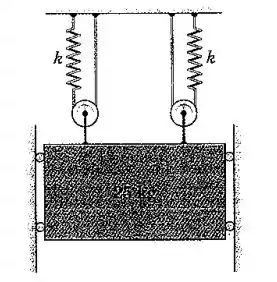
Pelo método dessa seção, determine o período de oscilação vertical. Cada mola possui uma rigidez de 1200 N/m, e a massa das polias pode ser desprezada.

Passo 1

Bom pessoal, nesta questão temos uma massa sustentada por duas polias. Vamos entender o que acontece com uma polia quando a massa se desloca x   para baixo:

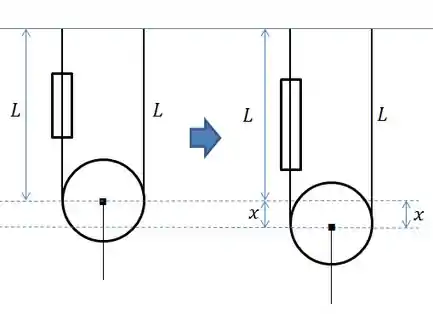
Quando a polia se desloca um comprimento x para baixo, os dois lados do também aumentam x . Considerando que o fio é inextensível, todo o deslocamento vai pra conta da mola. Então, somando o comprimento do fio antes e depois, temos o seguinte:

  E x t e n s ã o   d a   M o l a = L + x + L + x + π r - L + L + π r = 2 x

Como o sistema de molas está em paralelo, podemos calcular a constante equivalente:

k e q = k 1 + k 2 = 2 k

Passo 2

Agora, vamos utilizar o método de energia aprendido nesta seção do livro.

E = T + V

Onde:

T = 1 2 m x ˙ 2 ,   e n e r g i a   c i n é t i c a

V = 1 2 2 k 2 x 2 ,   e n e r g i a   p o t e n c i a l   e l á s t i c a

Portanto, a equação da energia do sistema fica:

E = 1 2 m x ˙ 2 + 4 k x 2

Considerando que o sistema é conservativo (não há perda de energia em função do tempo):

d E d t = 0

Substituindo o valor de E e derivando (lembrar da regra da cadeira):

d E d t = m x ˙ x ¨ + 8 k x x ˙ = 0

Arrumando esta EDO para o termo a segunda ficar com coeficiente unitário:

x ¨ + 8 k m x ˙ = 0

Olha só que sorte! Encontramos uma EDO na forma da equação do movimento harmônico simples. A frequência natural pode ser então escrita por:

ω n = 8 k m  

O período do movimento pode ser associado a frequência natural pela equação:

ω n = 2 π τ → τ = 2 π ω n

Agora é só substituir:

τ = 2 π 8 k m

Sendo m = 25   k g   e   k = 1200 N / m :

τ = 2 π 8 ( 1200 ) 25 = 0,321   s

Resposta

τ = 0,321   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de uma massa de 50g , em oscilação, é determinada pela relação x t =( 2,0c m )c o s ( 10 t - π / 4 ) , onde t está em s . Determine: a. A amplitude. b. O período. c. A constante elástica. d.
70. A amplitude de um oscilador com massa de 500g e período de 0,50s diminui em 2,0 % durante cada oscilação que ele efetua. a. Se a amplitude inicial for de 10c m , qual será a amplitude após 25 osci
O movimento de uma partícula é dado por x t = ( 25 c m )c o s ( 10 t ) , onde t está em s . Em que instante a energia cinética é duas vezes maior do que a energia potencial?
A Equação 14.25 estabelece que 1 2 k A 2 = 1 2 m v m á x 2 á . O que isso significa? Escreva algumas linhas explicando como se deve interpretar esta equação
A FIGURA Q14.7 mostra o diagrama de energia potencial e a curva de energia total de uma partícula que oscila presa a uma mola. a. Qual é o comprimento de equilíbrio da mola? b. Quais são os pontos de