Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Questões Conceituais - Ex. 7
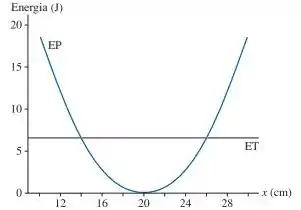
A FIGURA Q14.7 mostra o diagrama de energia potencial e a curva de energia total de uma partícula que oscila presa a uma mola.
a. Qual é o comprimento de equilíbrio da mola?
b. Quais são os pontos de retorno do movimento? Explique.
c. Qual é a energia cinética máxima da partícula?
d. Quais serão os pontos de retorno se a energia total da partícula for duplicada?
Passo 1
Em um movimento de um corpo de massa presa a uma mola de constante elástica , temos a conservação da energia. Assim, sendo a energia total, durante qualquer ponto da trajetória deveremos ter:
onde é a posição de equilíbrio da mola.
Passo 2
- A posição de equilíbrio ocorre quando a energia potencial elástica é nula. Pelo gráfico, vemos que isso ocorre para . Logo, o comprimento de equilíbrio da mola é de .
- Os pontos de retorno ocorrem quando . Pela equação dada acima, vemos que isso ocorre quando a energia potencial possui o mesmo valor da energia total. Pelo gráfico, vemos que isso ocorre em e .
- A energia cinética máxima ocorre quando é mínimo (ou seja, ). Assim,
- Quando a energia total dobra, temos:
Passo 3
Passo 4
Passo 5
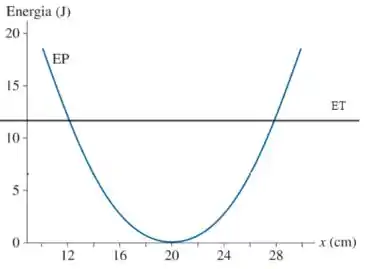
Nesse caso, vemos que a curva da energia potencial intercepta a energia total nos pontos e .
Resposta
- .
- e .
- .
- e .
Exercícios de Livros Relacionados
84. Para um certo oscilador, a força resultante sobre um corpo de massa m é dada por F x = - c x 3 . a ) Qual é a função energia potencial desse oscilador se considerarmos U = 0 para x = 0 ? b ) Um qu
Um deslizador de 200g , sobre um trilho de ar, está preso a uma mola. O deslizador é puxado por 10c m e liberado. Com um cronômetro, um estudante constata que 10 oscilações levam 12,0s para ser comple
A posição de uma massa de 50g , em oscilação, é determinada pela relação x t =( 2,0c m )c o s ( 10 t - π / 4 ) , onde t está em s . Determine: a. A amplitude. b. O período. c. A constante elástica. d.
70. A amplitude de um oscilador com massa de 500g e período de 0,50s diminui em 2,0 % durante cada oscilação que ele efetua. a. Se a amplitude inicial for de 10c m , qual será a amplitude após 25 osci
O movimento de uma partícula é dado por x t = ( 25 c m )c o s ( 10 t ) , onde t está em s . Em que instante a energia cinética é duas vezes maior do que a energia potencial?