Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 87

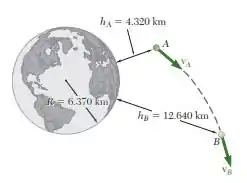
Sabendo que a velocidade de uma sonda espacial experimental lançada da Terra tem intensidade v A = 32,32 × 10 3   k m / h   no ponto A , determine a velocidade da sonda quando ela passar pelo ponto B .

Passo 1

Fala, galera. Beleza? Bora para mais um exercício de Dinâmica. Primeiro, para determinarmos a velocidade da sonda ao passar pelo ponto B . Para isso, vamos calcular a energia total no ponto A :

E A = T A + V A

Primeiro, vamos determinar a energia cinética em A :

T A = 1 2 m A v 2 = 1 2 m 32,32 × 10 3   k m / h 2

Vamos passar a velocidade para o SI, ou seja, para m / s :

T A = 1 2 m 8,98 × 10 3   m / s 2 T A = 40,32 × 10 6 ∙ m

Em seguida, vamos determinar a energia potencial no ponto A :

V A = - G M m r A = - g R 2 m r A V A = - 9,81 6370 2 m 6370 + 4320 k m V A = - 37,24 × 10 3 m

Passo 2

Agora, vamos fazer o mesmo para o ponto B . Vamos determinar a energia cinética em B :

T B = 1 2 m v B 2

E então, vamos determinar a energia potencial no ponto B :

V B = - G M m r B = - g R 2 m r B V B = - 9,81 6370 2 m 6370 + 12640 k m V B = 20,94 × 10 3 m

Por fim, para determinarmos a velocidade no ponto B   ( v B ) demos utilizar a variação de energia total entre A e B , que é nula. Temos:

∆ E = 0 E B - E A = 0 E A = E B T A + V A = T B + V B

Substituindo:

40,32 × 10 6 ∙ m - 37,24 × 10 3 m = 1 2 m v B 2 - 20,94 × 10 3 m v B = 7 × 10 3   m / s

É isso, galerinha. Bora praticar mais!

Resposta

v B = 7 × 10 3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pacote de 200 g é lançado para cima com uma velocidade v 0 por uma mola em A; ele se move em torno de uma estrutura sem atrito e é depositado em C. Para cada uma das estruturas mostradas nas figura
Uma bola de 1k g em A é suspensa por uma corda inextensível e tem velocidade inicial de 4,8 m / s . Se l = 0,6m e x B = 0 , determine y B de modo que a bola entre no cesto.
Prove que uma força F x , y , z é conservativa se, e somente se, as seguintes relações forem satisfeitas: ∂ F x ∂ y = ∂ F y ∂ x ∂ F y ∂ z = ∂ F z ∂ y ∂ F z ∂ x = ∂ F x ∂ z
A força F = x i + y j + z k x 2 + y 2 + z 2 3 / 2 age sobre uma partícula P x , y , z que se move no espaço. (a) Usando a relação deduzida no Problema 13.79, mostre que essa força é uma força conserva
(a) Calcule o trabalho feito de D a O para a força P do Problema 13.82 por integração ao longo da diagonal do cubo. (b) Usando o resultado obtido na resposta da parte b do Problema 13.82, verifique qu