Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 11.Problemas - Ex. 30

A  mola  da  balança  tem  um  comprimento  a quando  não  deformada.  Determine  o  ângulo  θ   de  equilíbrio quando o peso  W  é suportado na plataforma. Despreze  o  peso  dos  elementos. Que  valor  seria necessário para  W  a fim de manter a balança em  equilíbrio indiferente quando  θ = 0 ° ?

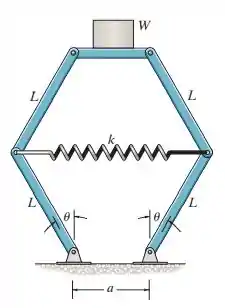
Passo 1

Fala aí, galerinha do Responde aí. Tudo beleza? Vamos fazer mais uma questão de Estática.

Sabemos que a energia potencial é positiva. Pela geometria, a mola vai estar localizada em:

x = 2 L sin ⁡ θ y = 2 L cos ⁡ θ

Então, a função de potencial vai ser:

V = V e + V g V = 1 2 k x 2 + W y V = 2 k L 2 sin 2 ⁡ θ + 2 W L cos ⁡ θ

Sabendo que a posição de equilíbrio é:

d V d θ = 0

d V d θ = 2 k L 2 sin 2 ⁡ θ + 2 W L cos ⁡ θ = 0 d V d θ = 2 k L 2 sin ⁡ 2 θ - 2 W L sin ⁡ θ = 0

Resolvendo esta equação, temos:

θ 1 = 0 θ 2 = cos - 1 ⁡ W 2 k L

Passo 2

Para determinarmos W , temos que obter a segunda derivada de V , e substituirmos em cada ângulo. Fica assim:

d 2 V d θ 2 = 4 k L 2 cos ⁡ 2 θ - 2 W L cos ⁡ θ

Logo, para θ 1 = 0 , temos:

W = 2 k L

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

W = 2 k L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O semicilindro de 10 N ≈ 1k g apoia o bloco que tem um peso específico γ = 13,5 k N m ³ . ³ Determine a altura h do bloco que produzirá equilíbrio indiferente na posição mostrada.
Uma ligação uniforme AB tem massa de 3 kg e está conectada nas duas extremidades por meio de pinos. A barra BD, com peso desprezível, passa por um bloco giratório em C. Se a mola tem uma rigidez k = 1
Determine os ângulos θ para haver equilíbrio do cilindro de 100 kg e investigue a estabilidade em cada posição. A mola tem uma rigidez de k = 6 k N m e um comprimento livre de 225 mm
Se uma carga l de 10 kg é colocada na panela, determine a posição x do bloco H de 0,75 kg para haver equilíbrio. A balança está em equilíbrio quando não há peso nem carga na balança.
Se o mecanismo está em equilíbrio quando θ = 30 º º, determine a massa da barra BBC. A mola tem uma rigidez k = 2 kN/m e está livre quando θ = 0 º º. Despreze a massa das ligações