Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 37

Se o mecanismo está em equilíbrio quando θ = 30 º , determine a massa da barra BBC. A mola tem uma rigidez k = 2 kN/m e está livre quando θ = 0 º . Despreze a massa das ligações

Passo 1

Desenhando o diagrama do corpo livre do corpo:

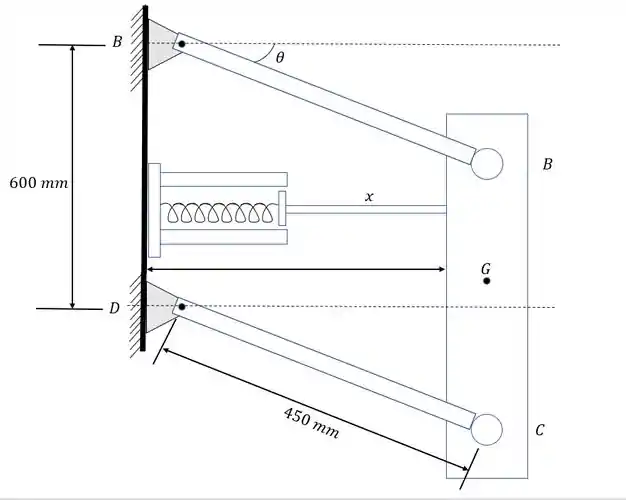
Passo 2

Da geometria da figura:

y 1 = G C - D C ⋅ s e n θ y 1 = 0,3 - 0,45 ⋅ s e n θ

x = A B ⋅ c o s θ x = 0,450 c o s θ

Passo 3

O próximo passo é calcular o enlongamento da mola:

s = x θ = 0 - x θ s = 0,45 - 0,45 ⋅ c o s θ s = 0,45 ( 1 - c o s θ )

Passo 4

Calculando as energias potenciais individuais do sistema:Barra BC:

V = m g y 1 = m ⋅ g ⋅ ( 0,3 - 0,45 s e n θ ) Mola:

V s = 1 2 k ⋅ s 2 = 2000 × 0,45 1 - c o s θ 2 V s = 202,5 ( 1 - c o s θ ) ²  

Passo 5

Obtento a expressão da energia potencial total do sistema, temos:

V = m ⋅ g ⋅ 0,3 - 0,45 ⋅ s e n θ + 202,5 ( 1 - cos ⁡ θ )   2 d V d θ = - m ⋅ g ⋅ 0,45 ⋅ c o s θ + 202,5 × 2 1 - c o s θ s e n θ d V d θ = - m ⋅ 9,81 ⋅ 0,45 ⋅ c o s θ + 405 s e n θ - 405 s e n θ c o s θ

Para a posição de equilíbrio θ = 30 º - m ⋅ 9,81 ⋅ 0,45 ⋅ c o s θ + 405 s e n θ - 405 s e n θ c o s θ = 0 m = 405 s e n θ - s e n θ c o s θ 9,81 × 0,45 × c o s θ = 7,10   k g

Resposta

m = 7,10   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras estão presas a uma única mola de constante k que está indeformada quando as barras estão na vertical. Determine o intervalo de valores de P para os quais o equilíbrio do sistema é estável
O elemento uniforme  A B  tem massa de  3   k g   e está conectado nas duas extremidades por meio de  pinos. O elemento  B D , com peso desprezível, passa  por um bloco articulado em  C . Se a mola te
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 12 sin ⁡ 2 θ + 15 cos ⁡ θ ) J , onde  0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 8 x 3 - 2 x 2 - 10 ) J , onde  x é dado em metros, determine as posições de equilíbrio e investigue a estabilid
A  mola  da  balança  tem  um  comprimento  a quando  não  deformada.  Determine  o  ângulo  θ   de  equilíbrio quando o peso  W  é suportado na plataforma. Despreze  o  peso  dos  elementos. Que  val