Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 153
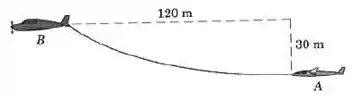
O planador A está sendo rebocado em um voo a altura constante e está 120 m atrás e 30 m abaixo do avião B. A tangente ao cabo no planador é horizontal. O cabo tem uma massa de 0,750 kg por metro de comprimento. Calcule a força trativa horizontal no cabo junto ao planador. Despreze a resistência do ar e compare o resultado com aquele obtido quando se aproxima a forma do cabo por uma parábola.
Passo 1
Primeiro vamos anotar as informações que a questão e a imagem nos oferecem, para facilitar a visualização:
A figura abaixo representa o esquemático da questão:
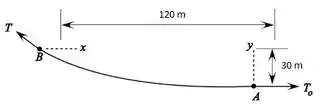
Agora, vamos lembrar a equação da curva formada pelo cabo abaixo:
Sabemos que:
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira, temos:
Resolvendo a equação acima, teremos que:
Passo 3
Lembre-se que a forma do cabo por uma parábola é dada por:
Sabendo disso, podemos aproximar, de tal modo que:
Então,
Logo,